Экономическая физика.

К разделам сайта:          Домой        Примеры       Теория индексов      Банки     

Содержание.

Введение.

ГЛАВА 1. Кинематика.

                1.1. Кинематика объекта как точки.

                1.1.1. Количество, качество, время.

                1.1.2. Движение, скорость, ускорение.

                1.1.3. Связь темпов роста и прироста с динамическими характеристиками движения.

                1.1.4. Аффинные пространства.

                1.1.5. Принцип суперпозиции.

                1.1.6. Понятие о сопутствующей системе координат. Переменные Эйлера и

                          переменные Лагранжа.   

                1.1.7. Разложение скорости и ускорения объекта по осям натурального трёхгранника Френе.

                1.1.8. Описание эволюции в многомерных пространствах (n ≥ 3).

                1.1.7. Динамические характеристики в стационарном и нестационарном базисах.

ГЛАВА 1. КИНЕМАТИКА.

1.1. Кинематика объекта как точки.

1.1.1. Количество, качество, время.

Существование любого объекта окружающего нас мира мы определяем в пространстве и времени. Это относится и к социальным и экономическим объектам. Но если существование во времени экономических объектов легко объяснить, то наличие у них пространственных характеристик требует дополнительных определений. Будем исходить из того, что экономический объект нельзя описать без выделения у него каких либо факторов. Наличие данных факторов и поставим в соответствие пространству существования данного объекта. Если существование объекта рассматривается в некотором периоде времени T, то, очевидно, эти факторы будут функциями времени t Î T.

Когда речь идёт об объекте, мы подразумеваем, что речь идёт о некотором его состоянии. Для состояния объекта введём обозначение x. Тот факт, что в момент времени t Î T объект x находится в состоянии x запишем в виде x = x(t). Для множества допустимых состояний объекта в период времени T введём обозначение X.

Пусть x_o = x(t_o) и x = x(t) два произвольных допустимых состояния рассматриваемого объекта. Естественно считать, что эти состояния различные, хотя бы потому, что они существуют в разные моменты времени (t ¹ t_o). Для различия состояний введём обозначение x = x - x_o. Элемент x характеризует динамику объекта и по своей природе отличается от состояния x Î X. Допустимое множество таких величин обозначим X. Будем считать, что справедлива запись x = x_o + x. Здесь x_o, x Î X, x Î X. Множество X определим в качестве присоединённого допустимого множества переходов из одного состояния в другое состояния к допустимому множеству состояний X.

Отличие x и x рассмотрим на следующем простом примере. Пусть x и x_o- два различных состояния продуктового магазина. Состояние x стало отличаться от x_o после того, как в данный магазин завезли 15 мешков сахара. Величины x_o и x могут не поддаваться логическому описанию и  восприниматься лишь на интуитивном уровне. Величина же x  есть количественно q = 15 определённое качество Y (мешок сахара), или качественно Y определённое количество q: x = qY. Вполне естественно, величина q в данном процессе могла бы принять любое неотрицательное действительное значение. Например, имеет экономической смысл и величина q = 15 + 1/2. Здесь так же очевидно, что величину q можно определить так, чтобы она принимала отрицательные значения, поскольку в описание процесса можно включить и вывоз сахара в том же качестве Y, т.е. вывоз из магазина сахара в мешках.  Следовательно, при фиксированной качественной величине Y количественной характеристике q можно приписать любое действительное значение q Î K (в рассматриваемом случае К - поле действительных чисел). Для этой величины введём обозначение  |x| = ±q.

На основе определённого выше экономического смысла элементов множества X легко объяснить, что если a и b являются элементами множества X, то их сумма также является элементом того же множества, т.е. a + b Î X, и  тот факт, что операция сложения элементов множества X обладает свойствами:

a + b = b + a (коммутативность),

(a + b) + с = a + (b + c) (ассоциативность),

a + 0 = a (наличие нулевого элемента),

a + (-a) = 0 (наличие противоположного элемента),

где нулевой элемент 0 = 0Y, -a = -qY - противоположный элемент элементу a = qY. Разностью a - b элементов назовём элемент x Î X такой, что x + b = a Î X.

Пусть a = aY Î X определяет количество a продукции определённого вида Y, которое сегодня завезено в наш магазин. На завтра мы заказали завести этой продукции в n раз больше. По смыслу поставленной задачи существует величина b = na Î K, которая принимает положительное или отрицательное значение и найдётся такой элемент b множества X, что имет место равенства b = na = an = bY, т.е. в общем случае для элементов множества X справедлива операция умножения их на любое действительное число m Î K, b = ma. Если m = 0 или (и) a = 0, то b = 0. При этом, определённая так операция умножения на число очевидно обладает свойствами:

m(a + b) = ma + mb (дистрибутивность относительно элементов множества X),

(l + m)a = la + ma (дистрибутивность относительно сложения чисел),

l(ma) = (lm)a (ассоциативность),

1^.a = a (умножение на единицу).

Эти линейные операции на элементах множества X определяют данное множество как линейное пространство (или векторное пространство). В общем случае множество K называется полем, элементы  x Î X - векторами или точками векторного пространства X, а элементы m Î K - скалярами. Наибольшее применение в экономических приложениях имеют векторные пространства над полем действительных чисел R. Такие векторные пространства называются действительными (вещественными) пространствами. Векторное пространство X является присоединённым векторным пространством к множеству X. Элементы векторного пространства поддаются логическому осмысливанию. Они однозначно определены как с качественной, так и с количественной стороны. Элементы множества X определяются в данном случае интуитивно. Они могут не поддаваться количественному описанию и обладать множеством других свойств, которые не обязательно присущи элементам векторного пространства X. Векторное пространство является как бы тенью множества допустимых состояний. Однако, если у элементов множества X фиксировать только свойство элементов векторного пространства, то можно оба эти пространства отождествлять. Будем говорить, что векторное пространство X является j-отображением множества X и писать j: X ® X. Следовательно, x = j(x) = x - x_o. Отображение Ф: X´X ® X, x = Ф(x, x_o) = x_o + x, назовём параллельным переносом множества X на вектор x. Отсюда следует, что существует множество параллельных пространств и линейное пространство X, фиксированное точкой x_o, одно из них. Этот факт запишем в виде равенства Ф(x, x_o) = Ф(x)(x_o). Отображение Ф(x) называют параллельными переносами.

Отображение j: X ® X будет вложением, если каждый элемент из X имеет не более одного прообраза, т.е. если a = j(a) и b = j(b), то   из a = b следует a = b. Если каждый элемент из X имеет хотя бы один прообраз, то отображение называется наложением. Имея наложение j: X ® X часто говорят, что j - отображение X на X. Отображение, являющееся одновременно наложением и вложением называется взаимно однозначным. Вложение называют инъективным отображением, наложение - сюръекцией, а взаимно однозначное отображение - биекцией. Относительно отображения j: X ® X, исходя из приведённого выше экономического смысла, можно сказать, что если множество X является множеством различных продуктовых магазинов, то завести продукт одного и того же качества Y в одном и том же количестве q можно во многие из данных магазинов. Поэтому одна и та же точка множества X может быть прообразом некоторое подмножество элементов множества X. В то же время, можно полагать, что каждая точка пространства X имеет хотя бы один прообраз и, таким образом, отображение j: X ® X является сюръекцией.

Качественный признак Y характеризует всё множество элементов векторного пространства X. Он линейно упорядочивает  объекты по количественным величинам q содержания в них качества Y, как бы проектируя все состояния X на вещественную прямую так, что точке x_o, например, отвечает на данной числовой прямой точка q = 0 и  каждому состоянию x объекта из множества его допустимых состояний X, ставиться в соответствие определённая точка прямой. На этой прямой задано направление отсчёта и можно выбрать любую её точку за начало отсчёта, поскольку точка x_o – произвольная фиксированная точка множества X. Если на данной прямой задать масштаб отсчёта, то получаем числовую ось. Обычно числовая ось характеризуется единичным вектором e. Таким образом, каждому состоянию x из множества допустимых состояний X по заданному качеству Y на числовой прямой с единичным вектором e и началом отсчёта O ставится в соответствие прикреплённый к точке O вектор x = OQ = qe. В той или иной мере качеством Y обладают все элементы множества X. Фиксация свойства Y упорядочивает их по количественному содержанию этого свойства и ставит в соответствие X векторное пространство X, геометрическим образом которого в данном случае является числовая прямая R.

Зафиксируем теперь состояние x некоторого объекта из множества его допустимых состояний X. Выделим у него какое либо качество Y и рассмотрим изменение количества этого качества во времени t на временном интервале T. В этом случае любое состояние объекта становится функцией времени x = x(t). При фиксировании качества от времени будет зависеть только количественная характеристика q = q(t). Получим: x(t) = x_o + q(t)Y, или x(t) = x_o + q(t)e. Здесь вектор e = Y = 1Y является основой измерения выделенного свойства и называется базисным единичным вектором. Базисный вектор определяет направление числовой оси и единицу масштаба измерения количества данного качества в любом состоянии объекта. С "прикреплением часов" к числовой оси получаем простейшую систему отсчёта. В системе отсчёта свойство-время можно эволюцию количества данного фиксированного качества у объекта изучать графически в системе координат  tOq (см. рис.1.1).

Рис. 1.1. Динамика состояния объекта в системе отсчёта по его фиксированной  качественной характеристике.

Очевидно, что подобных систем отсчёта можно построить множество, в которых данный график эволюции объекта по данному качеству остаётся неизменным. Действительно, фиксирование точки x_o, которая определяла начало отсчёта на оси координат q, было произвольным. Произвольным является и точка начала локального отсчёта времени. Это говорит о том, что динамика объекта не зависит от того, какую точку мы берём за точку отсчёта на координатных осях системы отсчёта. Изменение физического состояния объекта меняться не будет, например, при переносе начала системы отсчёта в другую точку O', т.е. при сдвиге начала отсчёта: g₁(t, x) = (t + s, x + s), t + sÎ R, s Î X. График сохранится в том же виде и в случае, если начало отсчёта будет скользить с равномерной скоростью v вдоль качественной прямой, т.е. в случае преобразования  g₂(t, x) = ( t, x + vt). И, наконец, имея ввиду в дальнейшем введение системы отсчёта, опирающуюся на многомерную систему координат, включим сюда тот факт, что описание динамики сохранится при повороте системы координат:  g(t, x) = (t, Gx), G – ортогональное преобразование системы координат. Такие системы отсчёта называются инерциальными. В инерциальных системах все законы эволюции любых явлений природы во все моменты времени одинаковы и все системы координат, движущиеся относительно инерциальной системы координат равномерно и прямолинейно, инерциальные. Отметим, что эти свойства составляют основной принцип классической механики, принцип относительности Галилея. 

1.1.2. Движение, скорость, ускорение.

Назовём движением объекта любое изменение его положения в фиксированном пространстве допустимых состояний X.  Если x_o и x - два состояния объекта и для объекта допустим переход из состояния x_o в состояние x, то из предыдущего следует, что таким переходом будет вектор x = x - x_o = qY. Вектор x характеризует изменение положения объекта и по определению является движением. Из предыдущего следует, что движение может быть обусловлено либо качественным его изменением, т.е. изменением только его свойства Y, либо количественным изменением фиксированного у него качества - изменением количественной величины q, либо изменением и того, и другого. Пусть движение определяется изменением некоторого параметра. Этот параметр обозначим t и будем рассматривать его в качестве глобального времени.  Состоянию x_o поставим в соответствие значение t_o глобального параметра, а состоянию x - значение t и введём локальный параметр s = t - t_o. Отметим прежде всего, что параметром движения может выступать сам количественный показатель q. Если полагать, что при изменении количественного показателя меняется качество объекта, то будем иметь: Y = Y(q), x(q) = qY(q). Очевидно, что и количество может зависеть от качества q = q(Y), т.е. может иметь место случай x(Y) = q(Y)Y, когда количество меняется при изменении только качества. От параметра t может зависеть только количественная характеристика, либо только качественная. Можно представить случай, когда от параметра t будут зависеть явно и качественная и количественная характеристики. Таким образом, в общем случае  движение можно рассматривать в виде  непрерывной по параметру t вектор-функции x(t) = q(t, Y(t))Y(t, q(t)).

Рассмотрим случай, когда параметр t меняется на интервале T действительной оси, X - множество допустимых состояний объекта, а X - присоединённое к нему векторное пространство. Тогда движением объекта на интервале T будет отображение x: T ®  X, x = x(t). Возьмём на интервале T две произвольные точки t_o и t, введём локальный параметр s: t = t_o + s. Разность (x(t) - x(t_o))/(t - t_o) = (x(t_o + s) - x(t_o))/s определяет величину движения, приходящуюся на единицу изменения параметра, или среднюю скорость движения на интервале [t_o, t] Ì T. При переходе к пределу при s ® 0 получаем вектор мгновенной скорости эволюции объекта в точке t_o: u(t_o) = lim(x(t_o + s) - x(t_o))/s = x'(t_o). Здесь введены обозначения: u = dx/dt = x'. Следовательно, x - x_o = x = su + a(s), где a(s)/s ® 0 при s ® 0, и в первом приближении x = su. Отсюда следует, что u Î X.  

Таким образом по определению движение есть переход из одного состояния в другое.  Величина движения в единицу времени называется скоростью движения. Отсюда следует, что скорость есть приращение движения в единицу времени. Приращение же скорости в единицу времени называется ускорением. Введём для ускорения обозначение w. Как и скорость, ускорение будет главным членом разложения скорости u = sw по малому параметру s и тоже является элементом w векторного пространства X. Для ускорения получаем выражение: w = du/dt = d²x/dt² = x''(t_o). Если в состояние x(t) осуществлён переход из состояния x(t_o), то, используя формулу Тейлора, имеем представление x(t) = x(t_o) + su(t_o) + s²/2 w(t_o) +o(s²), т.е. x(t) = su(t_o) + s²/2 w(t_o) +o(s²).

Таким образом, все три параметра движения объекта: пройденный путь x по траектории эволюции за данный промежуток времени s, скорость перемещения объекта u и величина изменения скорости w при этом перемещении, принадлежат векторному пространству X и представление в данном пространстве перемещения x в виде суммы x = su + s²/2 w является приближённым. Это представление будет тем точнее, чем меньше будет рассматриваемый здесь промежуток времени s.

1.1.3. Связь темпов роста и прироста с динамическими характеристиками движения.

Подражая гипотезе Р. Хаббарда, для понимания поведения объекта будем рассматривать множество его возможных состояний X и присоединенное к нему векторное пространство X в качестве двух существенных взаимно дополнительных взаимосвязанных и обуславливающих друг друга блоков. В пространстве X как бы действует "аналитический ум", который каждому возможному состоянию x объекта даёт "достоверную" информацию и размещает его в пространстве X "реактивного ума", в память. В свою очередь, каждое взятое из множества X состояние объекта в пространстве X подвергается оценке и упорядочивается на соответствующей шкале пространства X. Отключение при анализе поведения объекта пространства X вносит в поведение исследователя такой же эффект, как сон. Приводит к вседозволенности и абсурду, какими являлись, например, модные сравнения уровней жизни по отношению к различным периодам экономического развития нашего общества: к тринадцатому, сороковому годам прошлого века. Особенно обострившиеся к началу "перестройки". Приводит к отрыву формы от содержания.

Таким образом, чтобы сравнить два состояния x₁ и x₂ из множества X по содержанию у них некоторого качества Y, нужно на данном множестве зафиксировать произвольную точку x_o и перейти к элементам x₁ = x₁ - x_o и x₂ = x₂  - x_o пространства  X, на котором уже действует некоторое отображение f: X ® R, например, ставящее каждому вектору x = qY его числовую характеристику q = f(x) априори определённого качества Y. Определив величины q₁ = f(x₁) и q₂ = f(x₂) одного и того же качества Y, можно сделать оценку изменения величины этого качества при переходе из состояния x₁ в состояние x₂ на соответствующей шкале, например, на шкале отношений с помощью показателя  l = q₂/q₁, который в экономическом анализе называется темпом роста, либо показателем темпов прироста m = l - 1 = (q₂ - q₁)/q₁ = Dq/q₁. Но, в данном случае q = su + s²w/2. И, следовательно, получаем l  = (u₂ + sw₂/2)/(u₁ + sw₁/2) и m  = (Du + sDw/2)/((u₁ + sw₁/2), где введены обозначения:  Du = u₂ - u₁, Dw = w₂ - w₁. В первом приближении имеем l  = u₂/u₁ и m  = Du/u₁.

1.1.4. Аффинные пространства.

Множество допустимых состояний X, присоединённое к нему векторное пространство X над полем K вместе со множеством допустимых переходов Ф на множестве X называют аффинным пространством. Таким образом, аффинным пространством A является тройка (X, X, Ф), т.е. A = (X, X, Ф). Если на множестве допустимых состояний определены пространства X и Ф, то аффинным пространством иногда называют само множество допустимых состояний. В таком случае можно отметить, что векторное пространство X отличается от аффинного пространства X тем, что в нём фиксирована некоторая точка x Î X. Если x, y Î X, то при фиксированном x y = Ф(x, x) = x + x, т.е. имеет место отображение Ф: X´X ® X. Но, вместе с этим отображением существует и отображение Q: X´X ® X, x = Q(x, y), которое символически пока будем обозначать как разность y - x. Получаем, что для всех x и y принадлежащих множеству X y = Ф(x, Q(x, y)). При фиксированном x имеем  Q_x(y) = x. Отсюда y = Q_x^-1(x) = x + x =Ф(x)(x), т.е. Ф(x)(x) = Q_x^-1(x). Следовательно, Q(x, x) = 0, Q(y, x) = - Q(x, y), композиция Ф(- x) ◦ Ф(x) = Id_X - тождественному отображению на множестве X, Ф(x₁) ◦ Ф(x₂) = Ф(x₁ + x₂).

Рассмотрим возможность сравнения объектов в аффинном пространстве X по качественному свойству F. Этому свойству в соответствие поставим элементарный признак – единицу измерения данного свойства в возможных состояниях объекта, который определим единичным вектором e, который задаёт числовую ось R (см. рис. 1.2.).

Рис. 1.2. Геометрический смысл оценки состояния по заданному качеству.

Чтобы получить образ точки x на прямой R, нужно построить её ортогональную проекцию на эту прямую. Пусть такую задачу выполняет суръекция p: X ® R, которая в соответствии с выбранным масштабом измерения на R ставит каждому возможному состоянию x количественную оценку содержания в нём свойства F: q = p(x). Тогда гиперплоскость H = {x: p(x) = q}  в  пространстве X будет определять все состояния, которые содержат свойство F в количестве q, а подпространство Х_H всех прямых W не лежащих в этой гиперплоскости будет его дополнением. Образом всех точек плоскости H’ на R будет число q’ = p(y).

Поставим в соответствие переходному процессу из состояния x в состояние y образ Q(x, y) = p(y) – p(x) на числовой прямой R, которое соответствует величине вектора v =   le, где введено обозначение: l = q’ - q, и действие запишем в виде: F(v)(x) = F(x, Q(x, y)) = x + v. Будем иметь: y = x + v. При фиксированном x Î X отображение Q определяет биекцию Q_x: y  ® Q(x, y), X ® X. Получаем, что действие на множестве допустимых состояний X определяет транзитивную группу преобразований, которая задаётся выражением: F(u)(x) =  Q_x^-1(u).

Из транзитивности преобразований следует, что если x, y, z Î X, то для перехода из состояния x в состояние z = x + w, w = Q(x, z), можно осуществить сначала переход в состояние y = x + u, u = Q(x, y). А затем из состояния y сделать переход в состояние z = y + v, v = Q(y, z), т.е. z = x + (u + v). Если для операции композиции ввести обозначение “+”, то будем иметь: F(u) + F(v) = F(u + v), F(-u) + F(u) = Id_X - тождественное преобразование.

Таким образом, множество возможных переходных процессов X  как присоединённое к множеству допустимых состояний X раскладывается в прямую сумму X = R + H, где подпространство R характеризует изменение количества фиксированного свойства F в переходном процессе, а H – подпространство ортогонального дополнения. Если y = x +u, то  u = r + h Î X, r Î R, h Î H. Переход из состояния x в состояние y можно представить в виде y = x + r + h. Если функция Y характеризует некоторый измеритель данного свойства при таком переходе, то Y(u) =  Y(r) = (q’ - q)Y(e) и Y(h) = 0. Очевидно, здесь  выражение Y(e) играет роль масштабного множителя. Признак e характеризует свойство F. Поэтому данный масштабный измеритель в дальнейшем будем связывать непосредственно с этим свойством, т.е. отождествлять выражения Y(e) и Y(F) и писать Y(u) = (q’ - q)Y(F) = q’Y(F) - qY(F). Полагая Y(u) = Y(x’ -  x) = Y(x’) -  Y(x) и Y(x) = qY(F), заключаем, что каждому состоянию x Î X измерительная функция Y ставит в соответствие определённое число q Î R – количество содержания фиксированного свойства F в состоянии x.

1.1.5. Принцип суперпозиции.

Зафиксируем некоторую систему отсчёта. Пусть в этой системе отсчёта множество X состояний рассматриваемого объекта характеризуется уникальным свойством F, признаком которого служит вектор e. Предположим, что у данного объекта, можно выделить другое свойство F₁ с признаком e₁. В таком случае тот же объект будет в одно и тоже время определяться в двух различных признаковых пространствах  X и X₁. Из предыдущего следует, что  X = X₁ + H. Если предположить, что имеет место расслоение F = { F₁, F₂, …,  F_n}, то, применяя принцип математической индукции, получим: X = X₁ +  X₂ + … + X_n. Пусть данное расслоение представляет полную группу в том смысле, что никаких других свойств кроме уже выделенных у объекта больше нет. Тогда элемент x Î X будет разлагаться в прямую сумму x = x₁ + x₂ + … + x_n. Здесь x = qY(F) и  x_i = qⁱY(F_i). Считая, что для каждого свойства F_i применяется свой способ измерения его содержания  в свойстве F, т.е. Y(F_i) = Y_i(F), приходим к выражению

 qY(F) =  q¹Y₁(F) + q²Y₂(F) + … + qⁿY_n(F).

После деления обеих частей этого равенства на коэффициент левой части получаем для измерительной функции следующее представление:

Y =  l¹Y₁ + l²Y₂ + … + lⁿY_n.

Здесь Y_i – собственная измерительная функция i-го свойства, а lⁱ = qⁱ/q – собственное значение, отвечающее этой собственной функции, i Î N ={1, 2, …, n}. В теоретической физике последнее разложение является основным принципом квантовой механики – принципом суперпозиции состояний, а функция Y носит название волновой функции.

Очевидно, аналогичное  разложение по совокупности выделенного у объекта спектра элементарных признаков E_n = {e₁, e₂, …, e_n} имеет место и для его уникального свойства F

e = l¹e₁ + l²e₂ + …. + lⁿe_n.

Расслоение F = { F₁, F₂, …} может быть бесконечным. В таком случае и сумма e = l¹e₁ + l²e₂ + … будет бесконечной.

Пусть система E_n признаков имеет расслоение в соответствие с расслоением множества N = È{N_k:  k Î K = {1, 2, …}},    N_kÇN_l = Æ, где k ¹ l Î K. Введем новую систему функций Ф_k, связанную со старой системой измерительных функций условием 

                                                                        S m^kФ_k = S l^jY_j.

                                                                      ^{kÎK            jÎN}                    

Тогда разложение  

                                                                           Y = S  m^kФ_k,

                                                                                ^kÎK         

будет представлением функции Y в этой новой системе измерительных функций 

                                                                        Ф_k = å a^j_kY_j,

                                                                               ^jÎN_k                  

где введены обозначения: a^j_k = l^j/m^k. Новой системе функций будет отвечать и новая система элементарных признаков e_k = a^j_k e_j, j Î N_k, где e_k = Ф_k(F). Здесь Ф_k можно рассматривать как измерительную функцию более высокого уровня, которая получается в результате ряда локальных измерительных процессов Y_j, j Î N_k. Продолжая такой процесс детализации основного свойство объекта сверху вниз, приходим к сложной многоуровневой иерархической структуре объекта. Чем ниже мы спускаемся по такой иерархии, тем более детальным становится раскрытие действия объекта, чем выше мы поднимаемся, тем яснее становится смысл и назначение рассматриваемого объекта в целом. Множество N =È{N_k: N_k Î N = ¥, k Î K}может быть бесконечным, в то же самое время, множество K может быть конечным, т.е. имеют место равенства: e = l¹e₁ + l²e₂ + …. + lⁿe_n + ... = m¹e₁ + m²e₂ + …. + m^me_m. Здесь можно отметить проявление диалектической связи между конечным и бесконечным.

Таким образом, каждое свойство объекта определяет элемент в его иерархической структуре. Декомпозиция элементов объекта приводит к тому, что этот элемент становится как бы подобъектом исходного объекта, а последний рассматривается уже как система взаимосвязанных объектов, каждый из которых характеризуется своим уникальным свойством и подвержен, в общем случае, неограниченному расслоению. Например, в любой фирме можно выделить элементы по производственным, хозяйственным, финансовым  признакам. В свою очередь, в данных подразделениях имеет место расслоение по роду деятельности и т.п., вплоть до различия по занятиям спортом отдельных работников, их принадлежности различного рода партиям, социальным группам, привычкам.  

По отношению выделенного объекта (относительно его локального свойства) все остальные элементы образуют внешнюю, окружающую данный элемент-объект, среду. Ясно, что эта окружающая среда, так или иначе, воздействует на выделенный элемент, вызывает с его стороны ответную реакцию на эти воздействия, которая может вызвать не только изменения траектории эволюции элемента и структурные изменения в нём, но и структурные изменения в системе в целом, изменить траекторию эволюции внешней среды.

Из предыдущего следует, что для любого объекта x Î X можно определить некоторое свойство F и измерительную функцию этого свойства Y, с помощью которых объект (субъект) “проводит” измерения свойств у других объектов. Так, фиксируя состояние объекта в точке a Î X множества допустимых состояний, мы получаем квантованную измерительную функцию Y, которая на этом множестве определяет систему координат. С помощью этой функции можно описать любое другое состояние объекта. Действуя на состояние x Î X, эта функция играет роль оператора Y: X ® X, x = Y(x) =xⁱY_i(x) = xⁱe_i = (x¹, x², ..., xⁿ). Компоненты xⁱ называются координатами вектора x в системе координат, в которой элементарные свойства e_i = Y_i(x), i Î N = {1, 2, ..., n}, является базисными векторами. Поместив в эту систему координат часы, получаем n-мерную систему отсчёта.

 1.1.6. Понятие о сопутствующей системе координат. Переменные Эйлера и переменные Лагранжа.

Зафиксируем на множестве X произвольное состояние a. Выделим некоторое свойство F_a и определим “измерительный инструмент” Y_a этого свойства в других объектах-состояниях множества X. Пусть произвольный объект x Î X в момент времени t Î T находился в состоянии b = x(t), а к моменту времени t’ = t + s Î T он переходит в состояние c = x(t’) Î X. Здесь t глобальное время, отсчёт которого проводится от фиксированного состояния a = a(0) Î X. Отсчёт локального времени s ведётся от состояния b, в котором объект находился в момент времени t. Согласно изложенному выше, в состоянии x можно измерить содержание свойства F_a с локализацией его декомпозиции измерительными функциями  Y_ai  (i Î N_a = {1, 2, …, n(a)}):

Y_a(x) = x¹_aY_a1(F) + x²_aY_a2(F) + … + x^n(a)_aY_an(F) = xⁱ_aY_ai(F_a).

Здесь, в конце предыдущего раздела и в дальнейшем изложении материала применяется принятая в литературе сокращённая запись суммы по "немому" индексу, т.е. в данном случае, по индексу, который отсутствует в левой части (правило Энштейна).

Вводя обозначения x_a = Y_a(x) и учитывая равенства e_ai = Y_ai(F_a), получаем представление x_a = xⁱ_a e_ai.

Аналогичное представление можно получить, если отслеживать эволюцию объекта x из состояния b по свойству F_b измерительной функцией Y_b = (Y_bj: j Î N_b ={1, 2, …, n(b)}): x_b= x^j_be_bj. Очевидно, коэффициенты в правых частях представлений xⁱ_a = xⁱ_a(t), и x^j_b = x^j_b(s), (как координаты в соответствующих системах отсчёта одной и той же точки) функционально зависимы: xⁱ_a = fⁱ_a(x¹_b, x²_b, .., x^n(b)_b), i Î N_a. Если полагать, что функции в данном равенстве, по крайней мере, однозначно кусочно-дифференцируемы в каждой точке x = b, т.е. матрица Якоби J^a_b = det(¶(xⁱ_a)/¶( x^j_b)) этого преобразования является матрицей максимального ранга в точке x = b (rank J^a_b = min(n(a), n(b))), то существует обратная зависимость x^j_b = f^j_b(x¹_a, x²_a, .., x^n(a)_a), j Î N_b, которая так же является кусочно-дифференцируемой. Для удобства изложения в дальнейшем, функциональную зависимость будем записывать в виде: x_a = f_a(x_b).  

Совокупность переменных (s, x¹_b, x²_b, .., x^n(b)_b) носит название переменных Лагранжа. Эти переменные характеризуют эволюцию объекта в локальной системе координат, подвижной относительно глобальной системы координат, которая  связана с объектом a. Например, при наблюдении эволюции объекта на подмножестве S Ì X в заданном локальном промежутке времени. При этом само множество S на глобальном  отрезке времени совершает свою эволюцию. Будет естественным введение на множестве S локальной системы отсчёта. Изучить в этой локальной системе эволюцию объекта. А затем, если возникает необходимость, связать её с эволюцией системы в целом.

Совокупность переменных (t, x¹_a, x²_a, .., x^n(a)_a) носит название переменных Эйлера. Эти переменные применяются тогда, когда возникает проблема отслеживать эволюцию различных объектов, которые проходят определённое фиксированное состояние.

Введение сопутствующей системы координат следует ещё из того, что при удалении наблюдаемого объекта x от точки наблюдения a Î X свойство объекта F_x и изучаемое в нём свойство F_a, которое фиксирует глобальную систему координат, становятся настолько различны, что в данной системе координат фиксированная ранее качество объекта эволюция перестаёт наблюдаться. Примером может служить приближение эволюции объекта к эволюции в ортогональном подпространстве, т.е. в ортогональной к подпространству R плоскости H' (см. рис. 1.2.). Поэтому для изучения динамики объекта необходимо по мере накопления различий переносить начало системы координат в новую точку b Î X, построенная система координат в которой на основе нового свойства F_b делает динамику качества наблюдаемого объекта видимой в области S действия новой системы координат X_b Ì X. Такую подвижную систему координат называют сопутствующей. Здесь S рассматривается как подмножество аффинного пространства состояний X и оно само становиться аффинным пространством.

1.1.7. Разложение скорости и ускорения объекта по осям натурального трёхгранника Френе.

Движение объекта в пространстве определяется заданием зависимости x =x(t). Это выражение называется законом движения. В пространственно-временной структуре X ´ T закон движения определяет кривую эволюции объекта. Установим, как с этой кривой связаны такие характеристики движения как скорость и ускорение.

Во первых, от скорости и ускорения зависит длина пройденного пути объектом по его траектории эволюции. Очевидно существует и обратная зависимость, т.е. скорость и ускорение являются функциями пройденного пути объектом по кривой его эволюции. Но, тогда можно полагать, что скорость и ускорение зависят  и от формы этой кривой.

Зададим закон движения величиной пройденного пути объектом по траектории его эволюции s = f(t) и величину s пройденной пути объектом к моменту времени t, возьмём в качестве параметра движения объекта: x = x(s). Будем этот параметр называть натуральным. При таком описании движения скорость объекта в момент времени t Î T, отвечающей текущей точке M кривой, найдём по формуле

v = lim(Dx/Dt) = lim(Dx/Ds)lim(Ds/Dt) = (dx/ds)(ds/dt) = s't(s) Î X.

Здесь введены обозначения: s' =  ds/dt =df(t)/dt и t(s) = dx/ds.

Рис. 1.3. Трёхгранник Френе.

Предположим, что эволюция объекта проходит по плоской кривой L, лежащей в плоскости xMy (рис.1.3) и объект переходит из состояния M₁, отвечающего нулевому значению натурального параметра, в состояние M₂, соответствующему значению натурального параметра s + Ds. Тогда он проходит состояние M, которое назовём текущим состоянием. Будем считать, что текущее состояние отвечает значению натурального параметра, равному s (0 < s < s + Ds). Из рис.1.3 видим, что вектор Dx/Ds в пределе при Ds ® 0 направлен по касательной к кривой в точке M в сторону возрастания дуговой координаты s. Так как величины |Dx| и |Ds| эквивалентные бесконечно малые, то вектор t = dx/ds является единичным, dx =tds и x' = x + dx. С другой стороны, t(s) = v(s)/s' = v(f(t))/f'(t). Из равенства v = s't заключаем, что величина s' является модулем вектора скорости v.

В пространстве X введём внутреннюю бинарную симметрическую операцию (^.) - скалярное произведение элементов пространства X. Поскольку t единичный элемент пространства, то t^.t = t² = 1. Дифференцируя данное равенство, получим:

d(t²) = 2t^.dt/ds = 0.

Следовательно, элемент  dt/ds скалярного произведения либо равен нулю, либо ортогонален вектору t. По определению производной при  Ds ® 0 этот вектор равен

dt/ds = lim((t(s + Ds) - t(s))/Ds) = lim(Dt/Ds).

Но, вектор Dt лежит в плоскости xMy, значит и вектор dt/ds лежит в этой плоскости, ортогонален вектору t и, как видим из рис.1.3, направлен в сторону вогнутости кривой L. Единичный вектор n этого направления назовём главной нормалью кривой L в точке M, а плоскость xMy, содержащая векторы t и n, назовём соприкасающейся плоскостью. Если кривая плоская, то она лежит целиком в соприкасающейся плоскости. Так как векторы dt/ds и n коллинеарные, то dt/ds = Kn, где K - модуль вектора dt/ds.

При K = 0 найдётся такая достаточно малая окрестность точки M , в которой касательный вектор (или вектор скорости кривой) будет постоянным (с точностью до малых второго порядка относительно приращения Ds). Это значит, что в окрестности точки M траектория эволюции спрямляется и эволюция объекта на этом участке протекает с постоянной скоростью: s' = const, т.е. по линейному закону s = at + b по оси абсцисс Mx в направлении вектора t (с точностью до малых второго порядка относительно приращения Ds). Из предыдущего следует, что в таком случае на данном отрезке траектории эволюция объекта не претерпевает качественных изменений. 

Пусть K ¹ 0. Введём угол Dq(s) между векторами t(s) и t(s + Ds). Из рис.3 видим, что бесконечно малые величины Dq и Ds имеют один и тот же знак. Введение угла Dq позволяет представить предел в правой части предыдущего равенства в виде произведения двух пределов

dt/ds = lim(Dt/Ds) = lim(Dt/Dq)lim(Dq/Ds).

Из построенного на векторах t(s), t(s + Ds) и Dt треугольника находим |Dt| = 2sin(Dq/2). Следовательно, lim(|Dt|/|Dq|) = 1, отсюда получаем

 lim(Dt/Dq) = n, lim(Dq/Ds) = K,

или K = dq/ds, т.е. с точностью до малых второго порядка относительно приращения Ds коэффициент K свидетельствует об изменении направления эволюции и равен углу поворота вектора скорости на единицу проходимого пути. Это говорит о том, что при эволюции объекта по траектории L ось абсцисс поворачивается, изменяет своё направление. В эволюции объекта происходят качественные сдвиги и показателем этих структурных изменений является коэффициент К.

Геометрический смысл коэффициента K имеет для понимания эволюции объекта очень важное значение. Для выяснения этого смысла построим окружность L₁ с центром на оси ординат My в точке P и радиуса r = |MP| = 1/K. Эта окружность называется соприкасающейся окружностью или кругом кривизны, величина K - кривизной кривой в точке M, а  r - радиусом кривизны кривой L в точке M. Если через три точки  M₁, M и M₂ траектории L провести окружность и точки M₁ и M₂ устремить к точке M, то эта окружность в пределе совпадёт с соприкасающейся окружностью. Таким образом, с точностью до малых второго порядка Ds при K ¹ 0 траектория эволюции объекта L вблизи точки M может быть представлена дугой соприкасающейся окружности L₁.

Любые изменения в скорости эволюции объекта свидетельствуют о том, что эволюции присуще ускорение. Определяя ускорение как изменение скорости на единицу пройденного пути, находим

dv/dt = d(s't)/dt = s''t + s'(dt/ds)(ds/dt) = s''t + (s')²dt/ds = s''t + (s')²Kn.

Отсюда следует, что выражение для ускорения можно представить в виде суммы двух независимых друг от друга слагаемых

w = s''t + (s')²Kn,

которые составляют его проекции на орты подвижной системы координат xMy, с центром в текущей точке M плоской траектории L эволюции объекта. Коэффициент первого слагаемого s'' = d²s/dt² равен приращению скорости объекта в точке M его траектории эволюции, которое она получает по направлению оси Mx. Коэффициент второго слагаемого K(f'(t)/dt)² равен составляющей ускорения в направлении главной нормали кривой.

Для соприкасающейся плоскости xMy введём обозначение H. В этой плоскости лежит траектория L динамики объекта. Введём обозначение CH  для остальных элементов пространства X. Множество CH называется пространством ортогонального дополнения H в пространстве X. Очевидно, объединение элементов подпространств H и CH будет составлять всё пространство X. Это объединение называется прямой суммой. Для обозначения прямой суммы применяют специальное обозначение Å. Получаем разложение пространства X в прямую сумму: X = H Å CH. Любой элемент y пространства CH ортогонален любому элементу x пространства H: x^.y = 0.

Предположим, что точка M₂ совершает виртуальное смещение - отклоняется в пространство ортогонального дополнения CH. Траектория при этом начинает скручивается. Появляется отличная от нуля составляющая по оси Mz, с направляющим вектором b. Для её представления в общем виде, в пространстве H  введём новый объект - внешнее произведение векторов x Ù y, которое в  H служит аналогом вектора на прямой и является ориентированной площадью параллелограмма на H, построенного на произвольных составляющих его векторах x и y так, что y Ù x = -(x Ù y), и с площадью S = |x Ù y| = |x||y|sinj,  где j - угол между векторами x, y Î H. Внешнему произведению поставим в соответствие дополнительный вектор z  = (xÙy)^{^} Î CH и z^.x = 0, z^.y = 0, или бивектор. В нашем случае получаем z = x´y и b = (tÙn)^{^} = t´n Î CH.

Величина b^{^}=  tÙn Î H является внешним произведением единичных векторов и является единичным. Единичный вектор b ортогонален каждому свому составляющему вектору t и n и называется бинормалью. По аналогии с вычислением изменения направляющего вектора скорости t при эволюции объекта можно найти изменение вектора бинормали b. Очевидно, это будет подобное выражение, но с другим коэффициентом пропорциональности: db/ds = kn. Коэффициент k называется коэффициентом кручения. В случае k = 0 в окрестности текущей точки M кривой L найдётся такая достаточно малая окрестность, в которой траектория динамики объекта уплощается. Кривая на таком участке лежит в соприкасающейся плоскости. Если k ¹ 0, то кривая в точке M скручивается, уходит из соприкасающейся плоскости. При  k > 0 кривая уходит вверх от соприкасающейся плоскости в направлении вектора бинормали, а при  k < 0 - уходит под соприкасающуюся плоскость. И кривая становится пространственной.

Тройка векторов t, n и b определяет в пространстве X трёхмерную евклидову систему координат и подпространство R³ Í X, в которое проектируется траектория эволюции объекта. Динамику объекта в этом пространстве можно изучать по основным её характеристическим свойствам в понятном для нас естественном трёхмерном пространстве, точнее, в пространственно-временной структуре R³´T. Эта тройка векторов образует в пространстве X прямоугольный триэдр с вершиной в текущей точке M, называемый естественным, натуральным или подвижным трёхгранником Френе. Причём направления координатных осей t, n, b определяются точно также, как и направления координатных осей e₁, e₂, e₃ евклидовой системы координат. В этом трёхграннике имеются три координатные плоскости. С первой из этих плоскостей мы уже знакомы - это соприкасающаяся плоскость. В соприкасающейся плоскости лежат координатные орты t и n. Плоскость, построенная на ортах t и b, называется спрямляющей плоскостью, а плоскость содержащая векторы n и b - нормальной плоскостью. В нормальной плоскости лежат все нормали к кривой, проведённые к вершине триэдра.

Предположим, что помимо агрегатных свойств, описываемых признаками t, n и b, в динамике объекта обнаруживаются и другие свойства, т.е. выделенная группа признаков для описания динамики объекта не полна. Пространство, построенное на данных признаках, определим в качестве гиперплоскости пространства X и обозначим эту гиперплоскость, как и выше, символом H, а в пространстве X  дополнение к нему  обозначим  выражением CH. Снова будем иметь: X = H Å CH. В пространстве H внешним произведением t Ù n Ù b введём 3-вектор, который определим как правильно ориентированный единичный объём, и ортогональным дополнением к нему с = (t Ù n Ù b)^{^} введём единичный вектор  в пространстве ортогонального дополнения CH. Вектор с будет ортогонален каждому из векторов t, n, b. Векторы t, n, b и c определяют в пространстве X четырёхмерную евклидову систему координат и подпространство R⁴ Í X. В этом пространстве, как и в трёхмерном пространстве, можно изучать динамику объекта и для его траектории данные векторы будут составлять подвижный четырёхгранник Френе. То есть, в данном случае можно рассматривать динамику объекта в пространственно-временной структуре R⁴ ´ T. Естественным дальнейшим обобщение данного подхода будет рассмотрение эволюции объекта в пространстве R⁵ ´ T и т. д., введение пространственно- временной структуры Rⁿ ´ T, где n может быть любым натуральным числом.

1.1.8. Описание эволюции в многомерных пространствах (n ≥ 3).

В кинематике рассматривается движение объекта с геометрической точки зрения, без учёта причин, вызывающих изменение этого движения, так называемых сил. От геометрии кинематика отличается тем, что при рассмотрении эволюции в пространстве во внимание ещё принимается и время изменения положения объекта при данной эволюции. При обычном рассмотрении эволюции в такой пространственно-временной структуре считается, что время и пространство не взаимодействуют друг с другом, в каком бы направлении пространства объект наблюдения не двигался. Пространственно-временная структура принимается в качестве системы отсчёта. Состояние объекта в пространстве можно определить только по отношению состояния некоторого другого объекта, выбранного произвольно, но, в общем случае, неизменного, которое рассматривается как эталон. Систему отсчёта привязывают к этому неподвижному объекту и называют объектом отсчёта. Если объект относительно выбранной системы отсчёта не меняется, то говорят, что в данной системе отсчёта он покоится. Если же в выбранной системе отсчёта он меняется, то говорят, что объект движется. Таким образом, понятия "движения" и "покоя" являются относительными и имеют место только тогда, когда указана система отсчёта. Более того, в разных системах отсчёта движение носит совершенно разный характер.

Говорят, что движение объекта на некотором временном интервале T определено, если определено положение этого объекта относительно некоторой фиксированной системы отсчёта в любой момент времени t этого временного интервала. Из предыдущего следует, что задать движение можно естественным и координатным способом. При естественном способе требуется задание траектории относительно выбранной системы отсчёта; на траектории определить начало отсчёта дуги, положительное направление отсчёта и масштаб отсчёта. Движение будет задано, если для каждого момента времени t Î T будет известна величина s, указывающая положение текущей точки M на траектории L, т.е. если известен закон s = f(t) движения точки. Из определения движения следует, что функция f(t) однозначная, поскольку точка M не может находится одновременно в различных местах траектории. Во-вторых, т.к. движение процесс непрерывный, то данная функция непрерывная. Это значит, что бесконечно малому изменению её аргумента t отвечает бесконечно малое изменение переменной s. Более того, функция должна быть дифференцируемой - главная  часть её приращения  Ds при приращении аргумента Dt  должна быть однородной функцией относительно Dt.

Если s = c = const, то это означает, что данная точка неподвижна относительно рассматриваемой системы координат.

Закон движения может быть задан двумя способами: аналитически и графически. Графически закон движения задаётся в виде кривой в системе координат tOs (см. рис.1.4). Эта кривая называется графиком движения.

                                                          s

                                                        O                                                                             t

                                                                             Рис. 1.4. Закон движения.

При этом, траектория эволюции объекта, отвечающая данному закону движения, например в 3-мерном координатном пространстве, имеет свою форму кривой (см. рис.1.5).

                                                                                        z

                                                                                  a''

                                                                                                                                       A

                                                                                                                                 C

                                                                                                            M

                                                                                  b''

                                                                                   O            b'                                       a'          y

                                                                            a                    L

                                                                             B                                                 D

                                                                  b

                                                                 x

 Рис. 1.5. Кривая динамики объекта.

Отсюда видим, что закон движения и траектория динамики объекта - это разные элементы описания эволюции объекта. Закон движения может быть прямой линией, а траектория может быть какой угодно и наоборот.

При координатном способе задания эволюции объекта в системе координат задаются координаты q₁, q₂, ... текущей точки M траектории L как функции времени:

(1.1)                                                                                      q₁ = q₁(t), q₂ = q₂(t), ...

Эти функции должны быть однозначными, непрерывными и дифференцируемыми. Например, в трёхмерной декартовой системе координат (рис. 1.5) закон движения объекта задаётся в виде: x = x(t), y = y(t), z = z(t). Такой способ задания называется заданием движения в параметрической форме, а уравнения - параметрическими уравнениями кривой. Здесь параметром кривой служит время t. При данном способе описания движения наблюдения за поведением объекта осуществляется по эволюции проекций текущей точки его траектории на осях системы координат. Каждое из этих уравнений определяет закон движения проекции текущей точки на соответствующей оси. Движение объекта представляется  декомпозицией элементарных движений по трём (в трёхмерной декартовой системе координат) различным направлениям: на отрезке [a, b], на отрезке [b', a'] и отрезке [b'', a'']. А движение объекта в целом есть суперпозиция данных элементарных его движений по прямым.

Как правило, изучение поведения  экономического объекта осуществляется по его "фотографиям" в определённые моменты времени: t₁, t₂, и т.д. Математическое описание движения экономического объекта практически не отличается от описания объекта механической природы, но видеть движение экономического объекта так, например, как мы видим реальное движение объекта механической природы мало кому удавалось. Поэтому в анализе экономический объект всегда выступает в виде некоторой "математической" модели, в количественном  отражении определённого набора факторов в отчётности наблюдения. Например, о деятельности банка можно судить по следующим   данным (табл.1.1).                        

Здесь состояние объекта описывается четырьмя факторами: q_j (j = 1, 2, 3, 4), которые принимают значения на множестве t_i (i = 1, 2, ..., 12). Таким образом состояние объекта описывается матрицей Q₁ = ((q_ij)), размерности 12 ´ 4. Каждая строка этой матрицы описывает состояние объекта в определённый период времени. На данном уровне анализа такая информация может быть полной, т.е. полностью описывать деятельность объекта в границах постановки задачи. А может возникнуть необходимость в более детальном анализе. Появится потребность в декомпозиции отдельных факторов, привлечения дополнительной информации об объекте. Примером может служить следующее расширение табл. 1.1.

На этом уровне описания объект определяется уже шестью факторами и на соответствующем временном отрезке задаётся  матрицей Q₂ размерности 12 ´ 6. Очевидно, что для более детального изучения данного объекта наблюдения можно продолжить расслоение факторов и получить некоторый градуированный пучок Q_*: 0 ® Q₀ ® Q₁ ® Q₂ ® ... ® Q_n ® 0. Здесь отображение 0 ® Q₀  есть обычный указатель на объект, а отображение Q_n ® 0 указывает на то, что слой Q_n является самым нижним и самым подробным уровнем описания поведения объекта.

Таким образом описание поведения объекта может быть в пространстве одного, двух и т.д. измерений. Каждому измерению будет отвечать своя числовая ось. В общем случае такое расслоение может быть бесконечным (n ® ∞) и множество факторов, описывающих поведение объекта, может быть также бесконечным. В простейшем случае поведение объекта может описываться лишь одним фактором, на одной числовой оси.

Пусть описание объекта осуществляется одним фактором q, на одной метрической шкале, которую определим ортом e. Таким фактором при описании приведённого выше банка может быть капитал банка, т.е. фактор q₁ (q = q₁). На качественном уровне такому описанию будет соответствовать вектор x = qe Î X. Определим q как алгебраическую величину вектора x. Если пространство полно, то вектор x полностью определяет состояние объекта и его закон движения в виде уравнения q = f(t). Состоянию объекта можно в этом случае в соответствие поставить текущую точку M на числовой прямой Oq (рис. 1.6) c положительным или отрицательным значением в зависимости от направления отрезка |OM| = q.

                                           M'                            M₁                        M₂         

                                                                                                                                 q

                                                      O       e                         M

                                         Рис. 1.6. Прямолинейное движение объекта.   

Если абсолютная величина q возрастает, то движение называется прямым, в противном случае - возвратным. Если q = f(t) за всё время только возрастает либо только убывает, то движение называется монотонным. Если q не зависит от времени, то точка M не меняет своего положения относительно начала O координатной оси. В таком случае говорят, что объект находится в данной системе координат в покое. Если объект в момент времени t₁ находился в положении M₁, а в момент времени t₂ находится в положении M₂, то говорят, что за промежуток времени Dt = t₂ - t₁ объект совершил "перемещение" x = |M₁M₂|e. Перемещение в отличие от "пути" является вектором. Объект может за интервал времени T = [t₁, t₂] при переходе из положения M₁ в положение M₂ пройти разные пути, например, путь M₁M'M₂, тогда как перемещение будет одно и то же x. Понятия "перемещение" и "путь" совпадают только в случае монотонного движения.

Пусть точке M₁ отвечает координата q₁, а точке M₂ - координата q₂. Тогда алгебраическая величина перемещения будет равна Dq = |M₂M₁| = q₂ - q₁. С учётом того, что объект совершает перемещение из состояния M₁ в состояние M₂ за промежуток времени Dt, находим среднюю скорость движения за этот промежуток времени

v* = Dq / Dt = (q₂ - q₁) / (t₂ - t₁).

Если уменьшать промежуток времени Dt, устремляя его к нулю, то в пределе получим скорость перемещения объекта из текущего состояния M, или скорость объекта в момент времени t, который отвечает этому состоянию. Отсюда, по определению производной, получаем, что скорость перемещения объекта из состояния M равна выражению v = f'(t) = df(t)/dt.

Если на некотором участке движения координата и скорость имеют один и тот же знак, то объект удаляется от начала отсчёта и его движение является прямым. В противном случае объект приближается к началу отсчёта и его движение является обратным. Если скорость в некоторой точке t Î T обращается в нуль, то q = f(t) и этот момент имеет стационарное значение. При достижении в стационарной точке максимума или минимума объект меняет направление движения с прямого на обратное или наоборот. Если же скорость равна нулю на некотором интервале T₁ Ì T, то на этом интервале объект находится в покое. Если на некотором интервале  скорость постоянна, то движение на этом интервале называется равномерным. Закон равномерного движения при v = v₀, в начальный момент t = 0 которого объект находится в состоянии q₀,  имеет вид:

q = q₀ + v₀t.

В общем случае скорость  на интервале T является функцией времени v = v(t). Пусть в момент времени t₁ скорость движения объекта  равна v₁, а в момент времени t₂ скорость равна v₂. Определим приращение скорости Dv = v₂ - v₁ движения объекта на интервале Dt = t₂ - t₁ и вычислим на этом интервале среднее ускорение

w* = Dv / Dt = (v₂ - v₁) / (t₂ - t₁).

При Dt ® 0 находим ускорение движения объекта в произвольной точке t Î T

w = w(t) = lim(Dv / Dt) = dv/dt = d²q/dt².

В табл. 1.3 и на рис. 1.6 приведена динамика движения капитала банка, его скорости и ускорения.

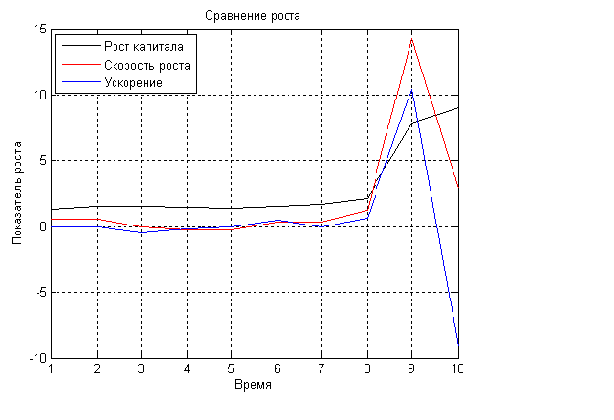
.1.6. Графики движения, скорости и ускорения.

Видим, что банк в 2005 год вступает с незначительной постоянной скоростью роста капитала. В летние месяцы направление движения капитала меняется на возвратное, затем наблюдается резкий рост капитала и опять происходит коррекция этого роста его возвратным  движением. Происходят, как бы, колебательные движения данного фактора около некоторой кривой роста. Такие колебательные процессы можно наблюдать во всех факторах этой системы, если не на разностях первого порядка (скорости), то на разностях более высоких порядков (ускорениях первого, второго и т.д. порядков). Подобные явления можно наблюдать в подавляющем большинстве экономических систем.

Движение, ускорение для которого постоянно, называется равномерно переменным. Скорость при равномерно переменном движении при w = a = const определяется выражением

v = v₀ + at,

а закон равномерного переменного прямолинейного движения будет иметь вид

q = q₀ + v₀t + at²/2.

Важным случаем прямолинейного движения являются гармонические колебания. Закон движения при гармонических колебаниях имеет вид

q = a sinwt.

Найдём скорость и ускорение объекта при гармонических колебаниях

v =dx/dt = aw coswt, w = d²q/dt² = -aw²sinwt = -w²q.

Величина a является наибольшей величиной отклонения от начала отсчёта на оси Oq, точка O называется центром колебаний, а промежуток времени, в течение которого объект возвращается в исходное положение после начала движения, называется периодом колебаний. Период колебаний можно найти из уравнений

sinw(t + T) = sinwt, cosw(t + T) = coswt.

Отсюда для периода колебаний получаем уравнение wT = 2p и находим период гармонических колебаний

T = 2p/w.

Обратная величина периода колебаний

 n = 1/T = w/2p

называется частотой колебаний. Аргумент синуса wt называется фазой колебаний, а величина w = 2pn - циклической или круговой частотой колебаний. В плоской системе отсчёта кривой расстояний при гармонических колебаниях является синусоида, кривой скоростей - косинусоида, а кривой ускорений - также косинусоида, но сдвинутая по фазе относительно графика движения на p.

В общем случае закон гармонических колебаний имеет вид

q = a sin(wt + a),

где величина a называется начальной фазой колебаний (фазой колебаний при t = 0). В частности, при a = 0 получаем закон гармонических колебаний с центром колебаний, совпадающим с началом O числовой оси q (рис. 1.6).

Движение точки -  проекции текущей точки траектории эволюции объекта на каждую ось системы координат может иметь достаточно сложный характер, а следовательно, траектория движения объекта в системе координат, например, в пространственной системе координат (рис. 1.5) может быть очень сложной кривой. Может иметь особые точки возврата, точки самопересечения. Если полагать, что уравнения задания движения (1) сколь угодно раз дифференцируемы, то любое уравнение  q_k = q_k(t) можно разрешить относительно переменной t и исключить эту переменную t из остальных уравнений. В случае, когда число уравнений равно n, после исключения получим систему из (n - 1)-го уравнения вида

(1.2)                                                                F_j(q_i, q_k) = 0, i = 1, .., k - 1, k + 1, ..., n; j = 1, 2, ..., n - 1.

Это параметрический способ задания движения. Здесь каждое уравнение F_j(q_i, q_k) = 0 представляет проекцию траектории на координатную плоскость q_iOq_k. 

Ещё один способ задания движения - задание положения текущей точки кривой её радиус-вектором, т.е. вектором r, исходящим из начала системы координат O в текущую точку M траектории движение объекта:

(1.3)                                                                                                r = r(t) = qⁱ(t)e_i.

Траекторией точки при этом способе задания движения будет годограф её радиус-вектора.

1.1.7. Динамические характеристики в стационарном и нестационарном базисах.