Анализ связи количества и качества на числовом примере системы банков

Домой        Примеры       Теория индексов      Банки      Физика

Обратимся к примеру предыдущего раздела, и покажем, что качество является при ранжировании явлений второй важной дополнительной характеристикой.

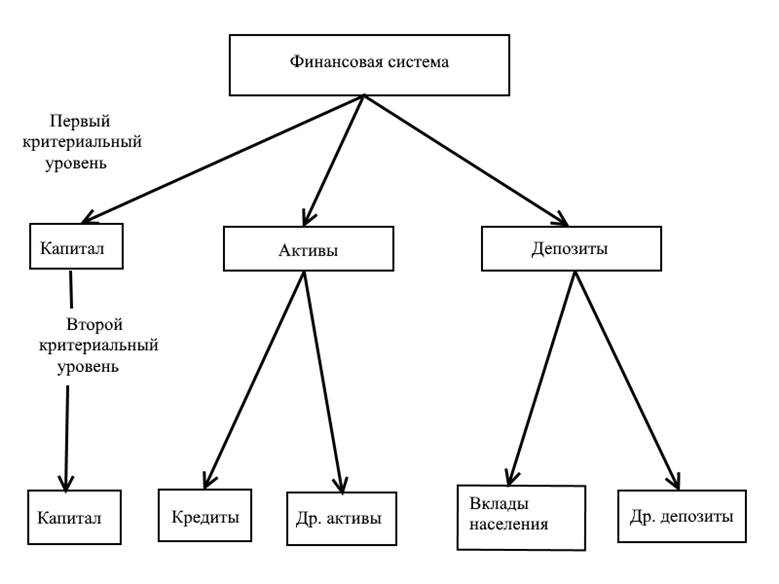
В данном примере представлена фиксированная в определённый момент времени система X, состоящая из шести объектов и определённая на множестве R действительных чисел. Каждый объект системы описывается в пространстве R⁵ – в пространстве пяти фиксированных качеств: капитал банка, кредиты, другие активы, вклады населения, другие депозиты. Для данного описания системы введём обозначение X⁵, X = X⁵. Но, как видим из её представления, данную систему можно описать и количеством факторов – капитал банка, активы, депозиты, т.е. в пространстве R³. Для описания состояния системы в этом пространстве введём обозначение X³. Здесь, как бы при таком сжатии показателей, одно пространство, пространство большей размерность, проектируется в другое пространство – пространство меньшей размерности, X⁵ ⊆ X³. Но, состояние объекта системы можно описать и одним рейтинговым числом. Для такого описания состояний введём пространство X¹. Получаем вложения X⁵ ⊆ X³ ⊆ X¹. В общем случае будем иметь: Xⁿ ⊆ X^n-1 ⊆ … ⊆ X¹.

Таблица 9.1.

Представление системы на первом уровне иерархии факторного описании.

Систему представим в виде двухуровневой иерархической структуры, где первый уровень её описания задан в табл. 9. 1.

Как и в предыдущем разделе в качестве эталона берём средние показатели факторов и переходим к относительно эталона значениям факторов. Получаем новую таблицу (табл. 9.2) с относительными величинами факторов.

Имеем вектор эталона s = [1.0000;1.0000;1.0000] и матрицу плотности

P = [0.3333      0         0;0         0.3333           0;0              0             0.3333].

В соответствие с табл. 9.2 построим расширенную матрицу

U = [B;s']

данных, включив в неё в качестве седьмой строки данные эталона и построим матрицу ковариаций

G = U*P*U'

и матрицу корреляций F(U). Здесь, и в дальнейшем, все операторы являются операторами MATLAB. Ниже представлен расчётный алгоритм F(U).

Рис. 9.1. Представление факторов системы двухуровневой иерархической структурой.

for k = 1:size(G,1)

       for l = 1:size(G,1)

          F(k,l) = G(k,l)/sqrt(G(k,k))/sqrt(G(l,l));

       end

   end

Таблица 9.2.

Описание объектов в относительных показателях.

F = [

    1.0000    0.8707    0.7483    0.7830    0.9501    0.8760    0.8823

    0.8707    1.0000    0.9711    0.8621    0.7187    0.9906    0.9948

    0.7483    0.9711    1.0000    0.7569    0.5972    0.9745    0.9725

    0.7830    0.8621    0.7569    1.0000    0.5521    0.7886    0.8114

    0.9501    0.7187    0.5972    0.5521    1.0000    0.7596    0.7579

    0.8760    0.9906    0.9745    0.7886    0.7596    1.0000    0.9993

    0.8823    0.9948    0.9725    0.8114    0.7579    0.9993    1.0000 ].

Матрица корреляций показывает тесноту связи объектов системы на первом критериальном уровне её описания. Чтобы выявить тесноту связей на уровне a, проведём матрицу корреляций к разреженной матрице, заменяя её большие a значения элементов единицей и полагая равными нулевым значения её остальных элементов. Получим при a = 0.90 матрицу H:

for k = 1:size(F,1)

      for l = 1:size(F,2)

            if F(k,l) > 0.90

                  H(k,l) =1;

            else

                  H(k,l) = 0;

           end

       end

end  

H = [

     1     0     0     0     1     0     0

     0     1     1     0     0     1     1

     0     1     1     0     0     1     1

     0     0     0     1     0     0     0

     1     0     0     0     1     0     0

     0     1     1     0     0     1     1

     0     1     1     0     0     1     1].

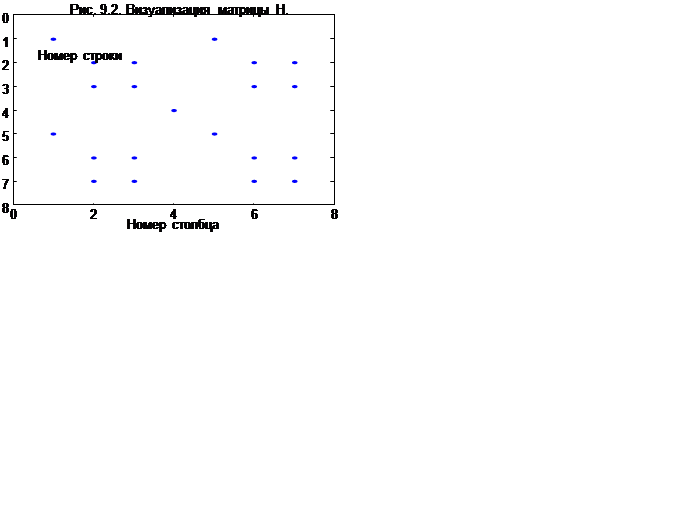
Визуализация данной матрицы представлена на рис. 9.2. и определяется оператором

spy(H)

Для наглядности групповой связи проведём DM-декомпозицию строк и столбцов (декомпозицию Далмейджа-Мендельсона) с учётом перестановки её строк p и столбцов q. Задавая значения параметру разряжения a, c одновременной декомпозицией по программе

for k = 1:size(F,1)

      for l = 1:size(F,1)

           if F(k,l) > a H(k,l) =1;

             else   H(k,l) = 0;

           end

     end

end

H = H

spy(H)  

[p,q,r,s] = dmperm(H)  

R = H(p,p);

subplot(1,2,1), spy(H);   subplot(1,2,2), spy(R)  

получаем наглядную картину качественной группировки объектов системы. При a = 0.90 имеем

H = [1     0     0     0     1     0     0;0     1     1     0     0     1     1;0     1     1     0     0     1     1;

         0     0     0     1     0     0     0;1     0     0     0     1     0     0;0     1     1     0     0     1     1;

         0     1     1     0     0     1     1]

p = [1   5   2   3   6   7   4],     q = [1   5   2   3   6   7   4], r = [1   3   7   8],  s = [1     3     7     8]

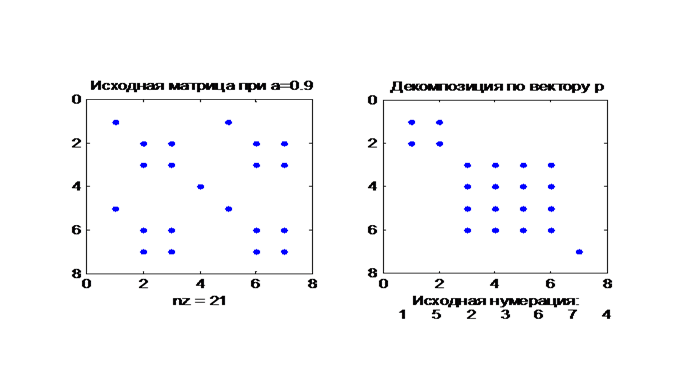
Рис. 9.3. Визуализация разреженной матрицы связей по исходному списку и по новому вектору декомпозиции p.

Здесь один изолированный объект и два блока (1, 5) и (2, 3, 6, 7). Если в табл. 9.1 каждую строку разделить на максимальный её элемент, то получаем табл.9.3, из которой хорошо видны качественные особенности объектов данных групп на первом критериальном уровне.

Сравнивая количественные характеристики объектов с качественными, построим список объектов в порядке роста их модульной оценки

4 5 2 1 7 6 3.

В силу того, что оценки качества квантуются циклически, их группы разместим в таком порядке

(4) (5 1) (2 7 6 3).

Отсюда заключаем, что качественная деятельность банков выделенной системы тесно связана с их мощностью. На данном уровне, образно, можно дать заключение, что с ростом мощности банка возрастает его внимание к депозитарной деятельности. Чем меньше мощность банка, тем больше его внимание активам. Например, банк под номером четыре разместил все свои средства в активы. В какие? Кредиты это, либо другие активы? – можно будет увидеть, переходя к анализу на более низком уровне в иерархической схеме, рис. 9.1, факторов описания деятельности. Именно ответ на данн��й вопрос позволит сделать заключение о деятельности да��ного банка.

Перейдём к анализу на второй критериальный уровень. На этом уровне иерархии система представлена матрицей B относительных данных (табл.

Таблица 9.3.

Масштабирование элементов групп координатным кубом [0, 1]³.

9.4), сравнение которых будем проводить в окрестности эталона s = [1;1;1;1;1] – вектор-столбец, с вероятностной матрицей плотности

P = eye(size(B,2))/size(B,2). 

Вычисления будем проводить по приведённой выше стандартной схеме. Построим расширенную матрицу U =[B s']. На её основе построим матрицу ковариаций G = U*P*U' и по алгоритму

for k = 1:size(G,1)

       for l = 1:size(G,1)

          F(k,l) = G(k,l)/sqrt(G(k,k))/sqrt(G(l,l));

       end

   end

корреляционную матрицу F:

    1.0000    0.7958    0.6622    0.7811    0.9209    0.8269    0.8176

    0.7958    1.0000    0.9771    0.7876    0.6725    0.9917    0.9963

    0.6622    0.9771    1.0000    0.6705    0.5530    0.9665    0.9725

    0.7811    0.7876    0.6705    1.0000    0.5776    0.7541    0.7606

    0.9209    0.6725    0.5530    0.5776    1.0000    0.7224    0.7108

    0.8269    0.9917    0.9665    0.7541    0.7224    1.0000    0.9988

    0.8176    0.9963    0.9725    0.7606    0.7108    0.9988    1.0000

Таблица 9.4.

Деятельность системы в относительных показателях.

Затем, на основе данной матрицы тесноты качественной связи, заданием показателя a, строим разреженную матрицу, к которой применяем декомпозицию Далмейджа-Мендельсона. Естественно, что на уровне связи a =0.90 получаем картину, изображённую на диаграмме, представленной на рис. 9.3. 

Дальнейший анализ можно проводить уже на уровне групп, полученных DM-композицией. Но, качественную картину можно наблюдать и на относительных пропорциях показателей описания объектов, которые получаются их отношением к наибольшему показателю из табл. 9.4. Для этого табл. 9.4 преобразуем по алгоритму

for k = 1:size(B,1)

       C(k,:) = B(k,:)/max(B(k,:));

end

Получаем табл.9.5. Из которой следует, что банк № 4 является небольшой кредитной организацией, вся деятельность которой сосредоточена на обслуживании кредитов. Банк под № 5 организован как хранилище капиталов. Это небольшие финансовые организации. Основная деятельность системы осуществляется банками № 3 и № 6. При этом, результаты деятельности банка № 6 практически полностью пропорциональны средним характеристикам системы, т.е. качество его деятельности практически на 100% совпадает с качеством деятельности системы в целом.

Таблица 9.5.

Деятельности объектов системы в пропорциях факторов.

В то время, как деятельность банка № 3 коррелируется с показателями системы в целом лишь на 97%. Если провести дополнительные качественный анализ, например, по пропорциям показателей (где вектор S отвечает банку № 6, а T – банку № 3)

  S =[0.9758         0.9129        0.9321               1.0000            0.8703]

 T = [0.4757         0.6576        0.7380               0.8668            1.0000]

и проделать следующие вычисления

x6 = ((S(1,1)+S(1,2)+S(1,2))-(S(1,4)+S(1,5)))/(S(1,1)+S(1,2)+S(1,2))*100

x6 = 33.2417

x3 = ((T(1,1)+T(1,2)+T(1,2))-(T(1,4)+T(1,5)))/(T(1,1)+T(1,2)+S(1,2))*100

x3 = -3.7093

то можно заметить, что ресурсы банка № 3 на 33% перекрывают депозиты, что обеспечивает надёжность этого банка. В то время как как у банка № 3 эти ресурсы такое покрытие не обеспечивают на 4%.

         матричная квантовая экономика