СОЦИАЛЬНАЯ ФИЗИКА

К разделам сайта:          Домой        Примеры       Теория индексов      Банки      Физика

        матричная квантовая экономика    

ОЦЕНКИ И СРАВНЕНИЕ МАССИВОВ В АНАЛИЗЕ ДАННЫХ.

В данной работе рассмотрен механизм построения количественной и качественной оценки больших многоэшелонированных структур, при описании которых применяются многомерные массивы, или многотомные книги. Такие массивы можно получить, например, бесконечной дезагрегацией (с фиксацией уровней) целеустремлённой системы (градуированный пучёк [1, 2]), применяемой при описании и оценке действия сложной иерархически структурированной организации [4], нейронных сетей [5], описываемых в категориях [6], методы решение которых с применением римановой метрики даются в работе [7], а с применением метрики симплектических пространств - в работе [8].

Терминологию и методы решения задач будем заимствовать из MATLAB [9]. 

Числовые массивы в современном анализе данных.  В современном анализе явлений в любой области человеческих знаний  - экономики и социологии, психологии, криминологии и медицине, наблюдения описываются цифровой информацией в виде прямоугольных таблиц, матриц. Таблицы отражают по существу состояния  предприятий, фирм, трудовых коллективов, личностный потенциал работника за многое годы. В большинстве случаев подобная информация не даёт возможности установить закономерности изменения состояний прямыми методами экономического, социального анализа и требует применения существенных абстрактных математических приёмов. Современные же математические методы и вычислительная техника позволяет обрабатывать числовую информацию в больших объёмах, с высокой точностью и большой скоростью.

Прямые методы анализа опираются на линейные модели, которые дают возможность проводить анализ, не отступая от смысловой интерпретации задачи. Однако решение на основе линейных моделей в большинстве случаев не даёт необходимой точности результатов. Возникает необходимость в построении нелинейных моделей, первым приближением которых, например, является применение моделей математической статистики. Если линейные задачи решаются в пространстве суммируемых функций (L₁), то решение вторых задач строится в пространстве функций, суммируемых с квадратом (L₂).  Моделирование задач в пространство L₂ даёт возможность не только использовать хорошо разработанные математические методы (например, такие, как методы гильбертова пространства), но и позволяет воспользоваться геометрическими методами интерпретации полученных решений.

Решение задач представляет некоторые оценки рассматриваемых моделируемых процессов, которые описывают их индикаторами (или относительными величинами). Такими индикаторами, например, при решении экономических задач являются базисные и цепные индексы. Известно, что если при описании явления существует хотя бы одна последовательность индикаторов, то можно построить множество последовательностей, которые описывают то же самое явление и построение которых гарантированно существованием множества строго монотонных функций. Так, если некоторый фактор или от него зависимый показатель имеют ускоренный рост, то для их наглядной интерпретации удобно перейти на логарифмическую шкалу измерения, если же наблюдаем их ускоренное замедление, то, наоборот, становится удобным сделать экспоненциальное преобразование соответствующей шкалы измерения. Таким образом, переход от одних индикаторов описания решения задачи к другим можно объяснить удобством интерпретации задачи в другой системе координат.

Как правило, наблюдения поведения объекта отражается в числовой информации, в которой состояния отражены в системе факторов его описания. При множестве наблюдений получаем прямоугольную числовую таблицу – двумерный массив действительных натуральных чисел, матрицу. Предполагая, что процесс наблюдения носит регулярный характер (к примеру, бухгалтерские отчёты деятельности некоторой фирмы), отчёты накапливаются в папку, страницы которой нумеруются. Получаем книгу, которая уже составляет трёхмерный массив. Постепенно полка заполняется папками – полку с папками можно полагать четырёхмерным массивом. Со временем такими книгами заполняются все полки данного стеллажа. Формируется массив пятой размерности и т.д. Приходим к понятию многомерных числовых массивов, в которых накапливается громадная информация. Естественно, что справиться с обработкой подобной информации можно, если её перевести на машинные носители. Для обработки такой информации, разработаны соответствующие математические методы.

Пусть двумерный числовой массив  имеет m строк и n столбцов. Его будем записывать в виде матрицы A_m´n, где m = |M|, n = |N|. Такие матрицы-сводки могут зависеть от временного фактора  t = T. Для трёхмерного массива введём обозначения

A =A(T, M, N).

Вызов элемента массива, находящегося, например, в таблице, соответствующей отчёту второго года наблюдения и стоящего на пересечении третьей строки и четвёртого столбца будем осуществлять по правилу

a = A(2, 3, 4).

В  экономических задачах, обычно, временной фактор градуирован, т.е. массив представляется в виде набора двумерных массивов занумерованных последовательностью натуральных чисел. Представленный выше массив называют трёхмерным.

Матрица – как двумерный числовой массив. Для построения оценок массивов рассмотрим широко распространённую  табличную форму различных производственных отчётных материалов, сформулировав её в виде некоторой затратной модели (см. табл. 1).

Таблица 1.   Характеристики производственного процесса.

Это модель некоторой производственной системы, конечным результатом деятельности которой является стоимость продукции.

Введём матрицу-столбец цен ресурсов

p = (p_j | j Î N),

и матрицу-столбец объектов

q = (q_i| i Î M).

Здесь введены множества N = (1, 2, …, n) и M = (1, 2, …, m).

Если ввести матрицу затрат

A = ((A_ij)),

где A_ij – затраты j-го ингредиента на выпуск изделий i-го вида, то данную модель производственного процесса можно записать в матричной форме

q = Ap.                                                                                   (1)     

Вектор q выступает в роли вектора оценок строк матрицы A в пространстве X^m. Его можно нормировать в пространстве l₁(X^m) суммируемых последовательностей, либо в пространстве l₂(X^m) последовательностей, суммируемых с квадратом.  Но, вектор p также можно рассматривать в качестве вектора оценок столбцов этой же матрицы. Имеем

                             q*q = p*(A*A)p,                                                                              (2)

где A* - эрмитово сопряжённая матрица матрицы A.

Из (1) находим

p = A⁺q.

Здесь A⁺ - псевдообратная матрица матрицы A. Умножая обе части данного равенства на произведение A*A и учитывая свойство псевдообратной матрицы [10, стр. 35]

A*AA⁺ = A*,

приходим к соотношению

(A*A)p = A*q,

подставляя которое в (2), будем иметь

q*q = p*A*q.                                                                                     (3)

Если полагать, что векторы p и q ортонормированы, то из равенства (3) получаем соотношения

p*A*q = q*q = p*p = 1,                                                                            (4)

из которого следует аналогичная (1) обратная зависимость

   p = A*q                                                                                       (5)

и которые вместе с нормой данных векторов в соответствующих пространствах

||q|| = (q*q)^1/2,     ||p|| = (p*p)^1/2

дают возможность вычислить норму оператора A

||A|| = (lim_||p||->1(p*A*Ap/p*p))^1/2.

Из соотношения

l = lim_||q||->1(q*AA*q/q*q)

находим, что

l = ||A||².

Отсюда следует, что векторы оценок столбцов p и строк q прямоугольной квадратной матрицы A с неотрицательными членами являются собственными векторами операторов A*A и AA* - симметричные квадратные матрицы с неотрицательными членами, отвечающие одному и тому же наибольшему собственному значению этих матриц, числу l, т.е. имеют место равенства

(A*A)p = lp,     (AA*)q = lq.                                                                    (6)

Бинарность (5) оценок одного и того же оператора  A вытекает из его материальной сущности - экономической (в данном случае, см. табл. 1), которая наделяет данный оператор двумя (и только двумя!) фундаментальными одинаково существенными и взаимно дополнительными структурными свойствами материи в любой её форме самоорганизации – количества и качества, и, таким образом, выражает симметрию этих свойств в виде равенств (1) и (5) [11, стр. 44].

Механизм построения оценок массива, заданного в виде прямоугольной матрицы, и сравнение двух массивов продемонстрируем на действительных матрицах A₁ и A₂, взятых из публичной печати,  и представленные таблицами 1 и 3 (см. Приложение 1).

Прежде всего, в данных массивах определим совокупность факторов  описания в их относительно независимом виде. Однако следует отметить, что поскольку система замкнута, то все факторы связаны друг с другом и изменение одного влияет на изменение другого. Но, в данном представлении в фактор "активы" включены "кредиты", а в фактор "депозиты" включены "вклады населения". Поэтому, пользуясь языком MATLAB, из столбцов исходной матрицы  A_i (i = 1, 2) сформируем новый массив A:

A = [A_i (:,1)  A_i (:, 3)  A_i (:, 2) – A_i (:, 3)  A_i (:, 5)  A_i (:, 4) – A_i (:, 5)  A_i (:, 6)].

Здесь факторы выступают в последовательности: "Капитал банка", "Кредиты",  "Другие активы", "Вклады населения", "Другие депозиты", "Прибыль". Получаем новую таблицу 1 , с другим описанием факторов и с новым массивом их значений в системе. Аналогично получаем табл.4 (см. приложения 1) с новым массивом данных.

Количественные оценки матрицы. Любой прямоугольный числовой массив A характеризуется двумя собственными  последовательностями индикаторов – последовательностью индикаторов оценок строк v и последовательностью индикаторов оценок  столбцов u, которые связаны с абсолютными величинами p и q зависимостями

u = q / ||A||,   v = p / ||A||,

а поскольку уравнения (6) однородные, то v и u будут собственными векторами операторов A*A и AA*, соответственно, отвечающие их наибольшим собственным значениям. После решения уравнений (6) искомые абсолютные оценки находим по формулам

p = ||A||v,    q = ||A||u.                                                                             (7)

  Таблица 1. Итоги деятельности банков Ростовской области на 01.07.04 (тыс. руб.)

Известно, что если существует хотя бы одна последовательность, например, оценок столбцов матрицы, то можно построить, опираясь на множество выпуклых функций, множество эквивалентных последовательностей оценок столбцов данного массива. Их эк��ивалентность можно обнаружить проекцией этих шка�� на одну из них. В таблицах 2 и 3 представлены оценки столбцов и строк  массива, приведённого в табл.1

Таблица 2. Оценки объектов.

Таблица 3. Оценки факторов.

в пространствах суммируемых последовательностей и суммируемых последовательностей с квадратом. Из табл.3 и 4 видим, что хотя численные значения на данных шкалах различны, их проекции на ранговую шкалу совпадают.

Таблица 4.  Оценка факторов в пространстве l₂.

X1 = Y1= 7.0302e+006                   Y2 = X2 = 1.3798e+007

Таблица 5.  Оценка объектов системы в пространстве l₂.

Эту же систему рассмотрим в другой момент времени, состояние в котором представлено массивом данных A₂ (табл. 3 приложения 1).

Переходя к новым факторам, получаем массив B₂ (табл.4 прилож.1).  Оценки факторов массивов B₁ и B₂ в пространстве l₂ приведены в таблице 4, где кроме оценок факторов помещены вероятности обнаружения этих факторов в общей деятельности системы.

Из табл. 4 находим, что хотя ранговые оценки факторов остались без изменения, в их относительных оценках произошёл сдвиг.   Существенные изменения произошли в активах системы и основном капитале. Заметные изменения произошли в прибыли. Но, можно отметить, что основные финансовые потоки системы проходят через активы (80%) и, хотя в активах произошли существенные изменения, вероятность  их присутствия в системе практически не изменилась, снизилась лишь на 0,84%:

(B1):  y₂ + y₃ = 0.7964,   (B2):   y₂ + y₃ = 0.78969.

Обратившись к табл. 5 заключаем, что в системе объектов произошли ранговые подвижки. Своё присутствие в системе укрепил банк "Центр-инвест", который более чем на 90% определяет состояние финансовой системы Ростовских банков. Чтобы оценить изменения в данных, нужно иметь, по крайней мере, два массива данных, из которых и можно выбрать измерительный эталон. В данном случае измерительным эталоном может служить как массив B₁, так и массив B₂, а агрегированные оценки структурных сдвигов можно строить с помощью индексов типа Ласпейреса

     L_y = y₂*y₁ / y₁*y₁,         L_x = x₂*x₁ / x₁*x_1,                                                    (7)   

или индексов типа Пааше

Y_y = y₂*y₂  / y₂*y₁,          Y_x = x₂*x₂ / x₂*x₁.                                                      (8) 

Учитывая равенства (3), получаем

L_y = y₂*y₁,              L_x = x₂*x₁.                                                                  (9)

Но,

s(x₁) = s(x₂) = s(y₁) = s(y₂) = 1

и, следовательно,

p_x = L_x²,             p_y = L_y²

суть вероятности  обнаружения сдвигов в оценках факторов и объектов за данный период наблюдения.

Из выражений находим

Y_y = 1 / L_y ,            Y_x = 1 / L_x.

Принимая массив B₁ за эталон, и используя оценки (9), будем иметь

L_y = 0.99455,      L_x = 0.97223,

т.е.

p_x = 0.94523,        p_y = 0.98913.

Видим, что при переходе системы из одного состояния в другое произошли незначительные (1,1%) качественные изменения. Эти изменения не отразились на шкале рангов (табл. 4). В то же время, произошли значительные количественные изменения, вероятность обнаружения которых равна 5,5%. В табл. 5 это отразилось в подвижки рангов.

 Чтобы отследить количественные изменения, разобьём диапазон вариации оценки объектов системы на количественной шкале, например, на четыре интервала. При этом объекты по количественной вероятностной оценке разобьём на четыре группы, как это показано в табл.6 для системы в состоянии А₁ (определённым в табл.2).

В табл. 6 система представлена двухуровневой иерархической структурой. На первом уровне она дана разбиением на группы по количественному признаку (мощности): малые, средние и крупные. В четвёртую группу выделяется объект, по мощности действия несоизмеримый с остальными, который определяет по внутренним оценкам системы 76% действия всей системы в целом.

Таблица 6. Группировка объектов системы в состоянии А₁.

Ниже, на рис.1, даётся структурная схема количественного расслоения системы в метрическом пространстве l₂, из которой следует, что

u = pⁱu_i

и

||u||² = pⁱ||u_i||²,

где p_i – вероятностная оценка присутствия соответствующей группы в системе.

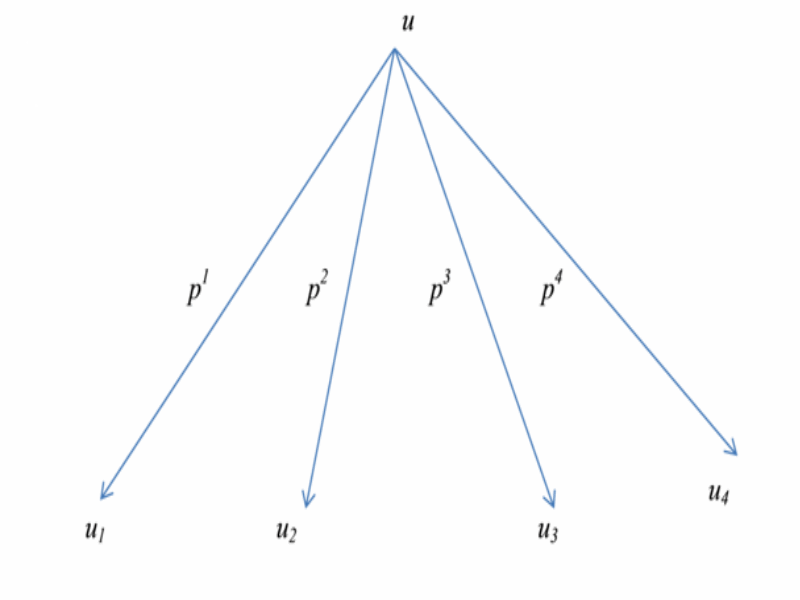
Рис.1. Расслоение системы по количественным признакам в пространстве l₂.

Оценки качества. Множество объектов (при этом, рассматривая множество состояний одного объекта как различные объекты) в n-мерном факторном пространстве будем рассматривать как аффинное пространство E. Если в этом пространстве фиксировать некоторый объект a в качестве начала координат, то оно превратится в n-мерное векторное пространство R, элемент x которого определяется как разность объектов x и a  аффинного пространства E

x = x – a,                                                                                     (10)

что определяет внешний закон композиции

x = a + x.

Наделяя окрестность фиксированной точки евклидовой структурой определением на элементах x, y векторного пространства R положительно-определённой билинейной симметрической формой m(x, y), можно ввести расстояние между точками x, y аффинного пространства

r(x, y) = ||y – x|| = ||x|| = m^1/2(x, x),                                                              (11)

связав, метрическим соотношением (10) аффинное и векторное пространства и поставив всякому объекту, достаточно близкому к фиксированному объекту аффинного пространства, во взаимно однозначное соответствие элемент векторного пространства.

Аффинный репер {a, x₁, x₂, …,x_n} в аффинном пространстве E порождает базис {x₁, x₂, …, x_n} присоединённого векторного пространства Rтакой, что координаты (a¹, a², …, aⁿ) точки x множества E в данном репере, где введены обозначения x_i = x_i – a, i  =1, 2, …, n, одновременно являются координатами вектора x = x – a в данном базисе

x = aⁱx_i.                                                                                   (12)

Если обозначить E_a векторное пространство, образованное элементами аффинного пространства E из окрестности произвольной точки a множества E, то отображение f_a: E -> R порождает естественный изоморфизм между векторным пространством R и векторизацией области E_a аффинного пространства E в точке a.

Установленный изоморфизм позволяет каждому объекту x аффинного пространства области E_a поставить во взаимно-однозначное соответствие его образ в векторном пространстве – вектор x, а паре объектов x, y из E_a – ковариацию их образов m(x, y). Например, путём сопоставления траекторий эволюции этих объектов из состояния a по угловому расхождению касательных к этим траекториям в их общей точке a. Таким образом, каждому состоянию x объекта подпространства E_a пространства E ставится в соответствие вектор

x = qY                                                                                          (13)

 из R, как количественная величина q = ||x|| определённого качества

Y  = x / ||x||

в ориентированном ��епером пространстве E_a. При этом dim R = dim E_a = n. 

         Очевидно,

D(Y) = m(Y, Y) = 1                                                                           (14)

 и при произвольном Y  уравнение (14) определяет в пространстве R единичную сферу S с центром в точке a.

Построим  последовательность нормированных базисных векторов W = (Y_j: j = 1, 2, ..., n). Если начала всех векторов системы W совместить с точкой a, то концы всех векторов Y_j  будут лежать на сфере S. Качественное сходство и расхождение любых двух векторов, исходящих из точки a будет определяться кратчайшей  дугой сферы, соединяющей концы их масштабных элементов (единичных векторов), в том числе и базисных векторов множества W.

  Все направляющие векторов-строк попадают в положительный шаровой  сектор единичного шара с центром в точке a. Концы этих векторов лежат на граничной сфере S единичного радиуса r.  Предположим, что вектор z является направляющим вектором оси шарового конуса. Представим его в барицентрических координатах базисных векторов

z = Y_ja ^j.

Конец данного вектора также лежит на сфере S.

В основу определения оценки расхождения любых двух векторов, выходящих из центра сферы и проходящих через шаровой конус, можно  положить множество различных критериев. Например, оценить длиной на��меньшей дуги большей окружности сферы, проходящей через данные точки и лежащей между этими точками, оценить хордой, стягивающей концы этой дуги, сделать оценку по площади параллелограмма, натянутого на направляющие данных векторов и т.п.

Пусть d_ij – длина хорды, стягивающей две точки Y_i, Y_j сферы S, а a_ij – длина дуги в радианах.  По теореме косинусов

d_ij² = D(Y_i) + D(Y_j) - 2s(Y_i)s(Y_j) cos a_ij.

Поскольку

D(Y_k) = s ²(Y_k) = 1,   k = i, j,

то имеем

cos a_ij = 1 – ½ d_ij².

Но, левая часть последнего равенства суть коэффициент ковариации данных векторов, коэффициент сходства. Отсюда заключаем, что чем меньше хорда,  тем больше сходство состояний, т.е. сходство и различие – антиномии, связанные некоторым тождеством. Для получения тождества найдём оценку бивектора, построенного на данных векторах

s(b_ij) = ||b_ij|| = |Y_i ˄Y_j| = s(Y_i)s(Y_j) sin a_ij = sin a_ij.

Из основного тригонометрического тождества, вводя соответственно меры сходства и различия объектов сферы

m(Y_i, Y_j) = cos a_ij,    n(Y_i, Y_j) =  sin a_ij,

приходим к метрическому тождеству

m ²(Y_i, Y_j) + n ²(Y_i, Y_j) = 1

на объектах сферы, а умножая данное тождество на произведение дисперсий

D(x, y) = D(x)D(y),

где

x = qY ,     y = pF,    Y, F Î W,

произвольные элементы метрического пространства R, приходим к основному метрическому тождеству (которое представим тождеством Пифагора)

s ²(x, y) = m ²(x, y) + n ²(x, y),

в котором внутреннее (скалярное) произведение векторов

m (x, y) = y*x

характеризует меру их сходства, а внешнее произведение

n ² (x, y) = |x ˄ y| ² = b*b = D(b),   b = x ˄ y,

меру их расхождения.

Рассмотрим n-мерное аффинное пространство E. Произвольно выберем в нём некоторую точку a и в окрестности E_a этой точки зафиксируем точки x, x_o, y, y_o. Пусть в этой окрестности  из точки x_o существует непрерывный путь в точку x, а из точки y_o – в точку y. Тогда можно соответствующие переходы записать в виде

x = x_o + x,   y = y_o + y,

где величины x и y будут элементами некоторого другого присоединённого к E_a  пространства R. В пространстве E_a всегда можно ввести топологию, которая обращает присоединённое пространство в векторное пространство. Эта топология индуцируется любой евклидовой метрикой

r(x_o, x) = s(x) >= 0,

где s(x) понимается как статистическая характеристика среднеквадратического отклонения состояния x от состояния x_o, а выражение

D(x) = s ²(x)

представляет дисперсию этого отклонения, которая вводится как внутреннее в R произведение

D(x) = x*x,

определяемое на RxR с помощью положительно определённой симметрической билинейной формы и которую символически будем записывать в виде

m(x, y) = y*x.

Таким образом, в основном метрическом тождестве реализуется единство таких диалектических антиномий как сходство и различие, качество и количество, форма и содержание и т.п.

Рассмотрим пространство B бивекторов. Учитывая свойства

x˄x = 0,      y˄x = - x˄y

можно определить его размерность

dim B = n(n/2 - 1)

и, если элементами векторного пространства присоединённого к евклидову пространству E_a  являются векторы, которые геометрически можно интерпретировать как направленные отрезки прямой, то геометрической интерпретацией элемента пространства B будет ориентированная площадь параллелограмма,  натянутая на бинарное соответствие (x, y) векторов пространства R.  Такое пространство называется симплектическим.

Как и в евклидовом пространстве в симплектическом пространстве мера порождается функцией

D(b) = b*b = (± s(b)) ²,

где s(b) – площадь соответствующего параллелограмма, а знак определяется ориентацией этой площади. Эта мера задаётся выбором евклидовой структуры в окрестности фиксированной точки a на аффинном пространстве E, которое при надлежащем выборе точек a превращается в риманово многообразие. Действительно, при выборе функции m(x, y) имеем

 D(b) = D(y) D(x) - m ²(x, y) = D(x˄y) = y*Kx

и можно ввести метрику m(a, b) в пространстве BхB на бивекторах a, b с помощью расширения основного метрического тождества

D(b)D(a) = m ²(a, b) + D(a˄b),

или, в общем случае,

D(a˄b) = b*Ka,                                                                                  (15)

где ядро представления является оператором со следующими конструктивными особенностями

K = K(a, b) = M(b, a) – M(a, b) = M* - M.

Здесь M – некоммутативный билинейный оператор,

M(a, b) = ab*,    M* = ba* = M(b, a),

который в квантовой физике [12, 13] определяется как произведение символов и несёт селективные свойства. Очевидно, если b = la, оператор Mстановится эрмитово-самосопряжённым и обращает оператор K в нуль, и наоборот, если K равен нулю, то M* = M.

Если элементам a поставить в соответствие обобщённое векторное пространство R, соответствующее аффинному пространству A, то обращение в нуль выражения (15) приводит к гомотетии [14, стр. 57]

b = a + la.  

Поскольку состояния объектов системы (банков) лежат в некотором конусе, а их качества характеризуются единичными векторами, исходящими из вершины этого конуса, то оценку качества можно сделать относительно положения соответствующего направляющего вектора оси конуса.

Разложим направляющий вектор оси конуса по базисным векторам векторного пространства присоединённого к пространству состояния объектов системы. В барицентрических координатах q^j, j = 1, 2,  ..., n,  это разложение принимает вид

z = q ^jY_j.

Тогда отклонение качества базисного вектора Y_j  от среднего качества системы z можно оценить функцией качественного сходства

m(z, Y_i) = Y_i^*z = r_ijq ^j = r_i ,

где для коэффициента вариации базисных векторов введено обозначение

r_ij = m(Y_j, Y_i).

Учитывая ограничение

D(z) = q*Rq = 1,

где R = ((r_ij)) – матрица коэффициентов ковариации, приходим к следующей задаче квадратического программирования

max{r_i = m(z, Y_i): D(z) =1, z >= 0}.

Предположим, что r = max (r_i: i = 1, 2, ..., n) решение данной задачи. Тогда подстановка

q = ry

сводит предыдущую задачу максимизации к задаче минимизации

min{F = y*Ry: Ry = 1, y ³ 0},

после решения которой находим

r = 1/(F)^1/2,    q = ry,  z = X*q,

где введено обозначение для матрицы нормированных данных

X = (Y₁;Y₂; …, Y_m)^T.

Для решения задачи квадратического программирования воспользуемся функцией quadprog MATLAB.

При постановке задачи квадратического программирования в общем виде

min{F = f *y + ½ y*Hy: Ay <= b, A_egy = b_eg, lb <= y <= ub}

решение получаем, если воспользуемся программой

[y, F] =quadprog(H, f, A, b, A_eg, b_eg, lb, ub).

В нашем случае

H =2R, f = 0, F = - R, b = - 1, A_eg = 0, lb = 0  

и

[y, F] = quadprog(2*R, [], - R, - b, [], [], lb)                                                               (16)

Находим вектор z 

z = (0.6839   0.1829   0.5414   0.3330   0.0810   0.2972)                                                (17)

и его корреляцию с векторами системы Y:

     1.  0.9668

     2.  0.8563

     3.  0.9268

     4.  0.9315

     5.  0.9431

     6.  0.8819

     7.  0.7961

     8.  0.8482

     9.  0.9211

    10.   0.9037

    11.   0.9729

    12.   0.7961

    13.   0.8214

    14.   0.9330

    15.   0.8688

    16.   0.9313

    17.   0.7961

    18.    0.8785

    19.    0.8869

    20.    0.8371

    21.    0.9844

    22.    0.8818

    23.    0.9170 

Видим, что на конической поверхности шарового сектора лежат объекты 7, 12 и 17. Эти объекты наиболее удалены по качественным признакам от среднего состояния системы. Наименьшее качественное отклонение от среднего имеют объекты 1, 11 и 21.

Условно по качественным признакам все объекты можно разбить на следующие группы.

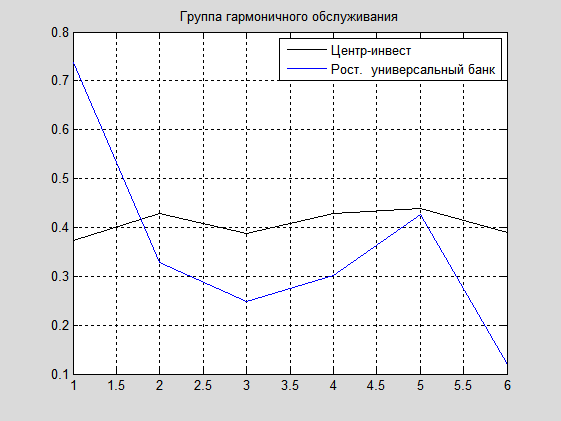
1.     Группа гармоничного обслуживания: Gr_1={Центр-инвест,  Рост.  универсальный банк}. Это банки, попадающие в подгруппы 4 и 1, соответственно. Их графики имеют вид

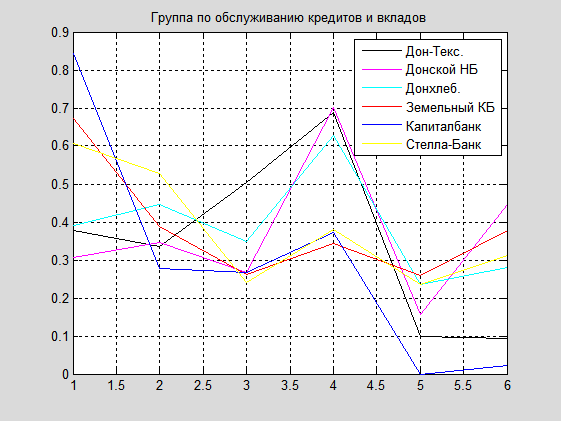
2.                Группа по обслуживанию кредитов и вкладов: Gr_2 = {Дон-Тексбанк, Донской народный банк, Донхлеббанк, Земельный КБ, Капиталбанк, Стелла-Банк,  Таганрогбанк}. Графики действия этих банков имеют вид

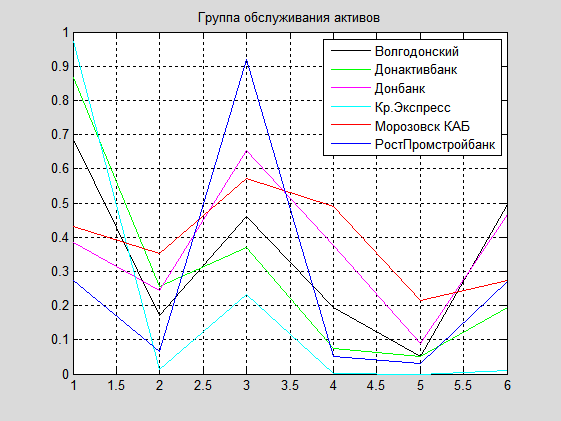
3.     Группа обслуживания активов: Gr_3={Волгодонский  ГКБ, Донактивбанк, Донбанк, Кредит Экспресс, Морозовсккомагробанк, РостПромстройбанк, Сельмашбанк}. Их графики изображены ниже.

4.     Группа обслуживания активов и вкладов: Gr_4={Донинвест,  Донкомбанк, ИБРР-банк, Южный регион, Южный Торговый Банк}.  Их графики изображены на следующем рисунке

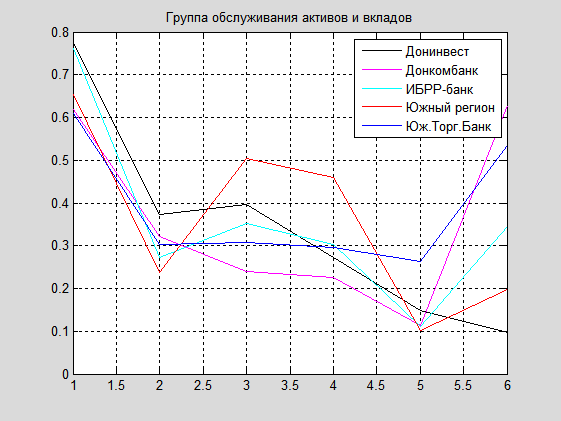
И последняя группа в качественном расслоении – это группа

5.     Группа обслуживания активов и депозитов юрлиц: Gr_5= {МеТраКомБанк,  Южный региональный банк}. Графики этих банков изображены на следующем рисунке

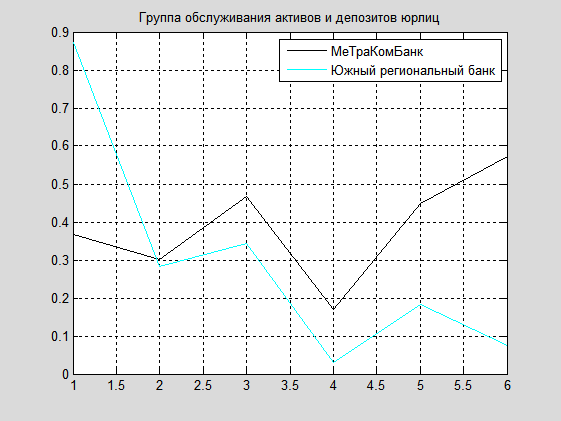
Естественно, что каждый объект имеет индивидуальные качественные особенности и занимает своё место в рассматриваемой финансовой системе.

Сравнение массивов. Изучая массивы, мы неизбежно приходим к задаче их сопоставления, сравнения отдельных их элементов и массивов в целом. При любом сравнении обязательно должен присутствовать измерительный эталон. При построении оценки отдельного массива уже был построен эталон для измерения качественных и количественных характеристик. При сравнении нескольких массивов можно воспользоваться тем же эталоном. Каждый массив может давать свой измерительный эталон и при сравнении множества массивов можно построить множество различных связанных друг с другом определёнными функциональными зависимостями измерительных эталонов.

   Сравним два массива A1 и A2, заданных данными в табл. 2 и табл. 4 приложения 1. Массив A1 был исследован выше. В качестве эталона был взят, удовлетворяющий условиям (6), вектор p оценки столбцов. Этот вектор и выберем в качестве эталона при сравнении данного множества массивов. С массивом  A2 сделаем те же операции, что и при анализе массива  A1. Элементы каждой её строки делим на соответствующие элементы эталона. Получаем новую матрицу X. А нормируя строки последней, получаем матрицу Xu, с помощью которой находим корреляционную матрицу объектов множества A2

R = Xu'*Xu.

Используя теперь решение задачи квадратического программирования, находим, что объекты 2, 14, 15, 20 наиболее удалены от оси

z₂ =(0.6839    0.1829    0.5414    0.3330    0.0810    0.2972)               (18)

нового конуса соцелей. Объектами же качественно близкими к среднему системы становятся объекты 5, 6, 18 и 21.

Если рассмотреть вероятности присутствия факторов в формировании действия системы относительно осевого вектора (см. табл. 4), то капитал банка и пассивы ведут себя достаточно консервативно, в то время как активы динамично меняются.

Таблица 4. Вероятности присутствия факторов в системе.

Качественное расхождение систем A₁ и A₂ определяется коэффициентом корреляции векторов (16) и (17) zz₂ = 0.9423, что в угловом измерении составляет приблизительно 20^o.

Рассмотрим корреляцию объектов систем с соответствующими направляющими осевых векторов (табл. 5).

Из табл.5 видим, что объекты качественно сблизились (конус качественного расхождения сузился на 5,5%) и ось конуса сместилась на 3,8^о, что свидетельствует о том, что произошедшие качественные сдвиги в структуре объектов незначительны. Эти сдвиги можно наблюдать на соответствующих графиках (см. прилож. 3).

Таблица 5. Коэффициенты корреляции субъектов систем с их направляющими векторами осей симметрии.

Литература.

1.     Бредон Г. Теория пучков /М., Наука, 1988.

2.     Бондал А.И. Представления ассоативных алгебр и когорентных пучков /Изв. АН СССР. Сер. матем., 1989,         том 53, выпуск 1, стр. 25-44.

3.     Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем /М., Мир, 1973.

4.     Кондрашов И.Е., Королёв C. MATLAB как система программирования научно-технических расчётов /М., Мир, 2002.

5. Хайкин С. Нейронные сети //М., С.-П., 2008.

6. Новиков Б.В. Лекции по теории категорий //Луганск, 2004.

7. Нейман И. Математические основы квантовой механики //М., Наука, 1964.

8. Дирак П.И.А. Лекции по квантовой механике//Ижевск, Ижевская республиканская типография, 1998.

9. Кондрашов В.Е., Королёв С., MATLAB, М., Мир, 2002.

10.     Гантмахер Ф.Р. Теория матриц //М., Наука, 1988.

11.     Идлис Г.М. Единство естествознания по Бору и единообразные взаимосвязанные периодические системы физики, химии, биологии и психологии /Исследования по истории физики и механики, 1990 //М., Наука, 1990.

12.     Грин Х. Матричная квантовая механика /М., 2009.

13.     Кемпфер Ф. Основные положения квантовой механики /М., 2007.

14.     Берже М. Геометрия, том первый М., Мир, 1984.