ОБЩАЯ ТЕОРИЯ СИСТЕМ

  1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.

Объект и система. В основу изложения материала положим категорию "объект", наблюдаемую, в её самом широком смысле как математический образ реальности действительности (объективной или субъективной), которая из окружающей среды выделяется определёнными свойствами. Таким образом объект выделясь из окружающей среды, является её частью и, как части окружающей среды, в нём также можно выделить определённым набором свойств подобъекты. Отсюда следует, что в таком понимании объект (субъект) и его подобъекты, как и внешняя среда и её объекты соотносятся как части и целое, подчиняющиеся общим принципам взаимодействия в силу общего свойства целостности. Это общее свойство целостности определяет нахождение элементов как вертикального, так и горизонтального расслоений в определённых связях друг с другом как целое составных частей – систему.

Системы и их многоуровневые иерархические расслоения. Примером системы является вселенная (рис. 1). Вертикальное познание вселенной ограничено только возможностями наблюдателя.

Рис.1.Вселенная (https://cdn.pixabay.com/photo/2015/11/15/08/15/universe-1044107__340.jpg)

На определённом уровне абстрагирования познания её элементы будем считать неделимыми, атомами, в силу понимания Демокритом. Такими атомами на соответствующем уровне абстрактного описания могут служить галактики (рис. 2). 

Рис. 2. Галактика "Млечный путь" (https://hi-news.ru/wp-content/uploads/2019/12/galaxy_spirale_image_one.jpg).

Различают много различных видов галактик по тому, как они организованы. Наиболее распространены спиральные галактики и именно к такому виду относится и наша. Кроме того, существуют кольцевые, эллиптические и др. Галактика может содержать в себе множество туманностей — как остатков взорвавшихся звёзд, так и регионов звездообразования.

Как видим, на горизонтальном уровне расслоения вселенной каждая галактика выделяется из ряда других объектов своими собственными свойствами. Одним из таких свойств, например, в галактике "Млечный путь" является присутствие в ней нашей солнечная системы. В свою очередь, каждая галактика является объектом, по отношению к которому вселенная является внешней средой и, галактика, как объект анализа, может быть подвержена дальнейшему расслоению.

Находим, что галактики – это звёздные системы. Например, одним из свойств в галактике "Млечный путь" является присутствие в ней звезды "Солнце", которая, как неделимый элемент, на данном уровне абстрагирования служит "атомом" галактики "Млечный путь".

Но, каждая звезда галактики сама является системой, если в её окрестности выделить присутствие других объектов, например, планет. Так, солнце содержит планетарную систему, представленную на рис.3. Это уже будет третьим уровнем в данной иерархии расслоения.

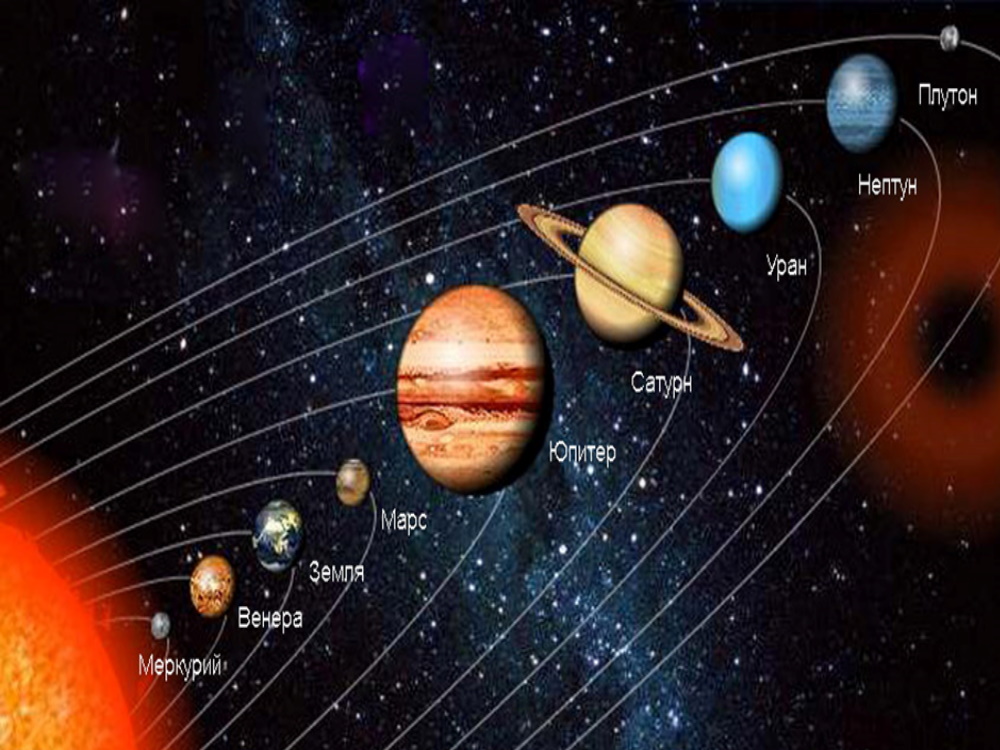
Рис.3. Планетарная система солнца (https://aboutspacejornal.net/wp-content/uploads/2016/01/586143-ss11.jpg).

Можно такое дифференцирование продолжать до микроуровня и дальше. Вероятно, пределом подобной дифференциации будет лишь возможности приборов наблюдателя.

Вселенная предстаёт в виде иерархической многослойной многоуровневой системы с разветвлённой горизонтальной структурой. Каждый выделенный элемент слоя добавляет новое уникальное свойство в описание агрегатного состояния объекта как целого. Очевидно, чем ниже по данной структуре опускаемся, тем более детальным становится описание системы. Чем выше поднимаемся по этой структурной лестнице, тем лучше становится её понимание в целом.

В таком представлении система описывается цепным комплексом 𝒦 = (K_*, ∂_*), в котором слои K_n образуют цепи объектов, а дифференциальные операторы ∂_n играют роль связей между элементами слоёв. С другой стороны, данный цепной комплекс представляет множество объектов и множество связей между ними. Подобные задачи возникают во всех областях знаний: в управлении, при распознавании образов, оценки состояния, вариантов выбора, при анализе данных, при обнаружении и преследовании целей и т.п.

В общей теории категорий цепной и коцепной комплексы относят к малым категориям поскольку семейство объектов и связей между ними являются множествами. Цепные комплексы изображаются в виде графов, различного рода диаграмм. В соответствие с теорией графов объекты 𝒦 называют вершинами, а связи – дугами. Пример комплекса из теории принятия решений, представленного неориентированным графом, приведён на рис.5.

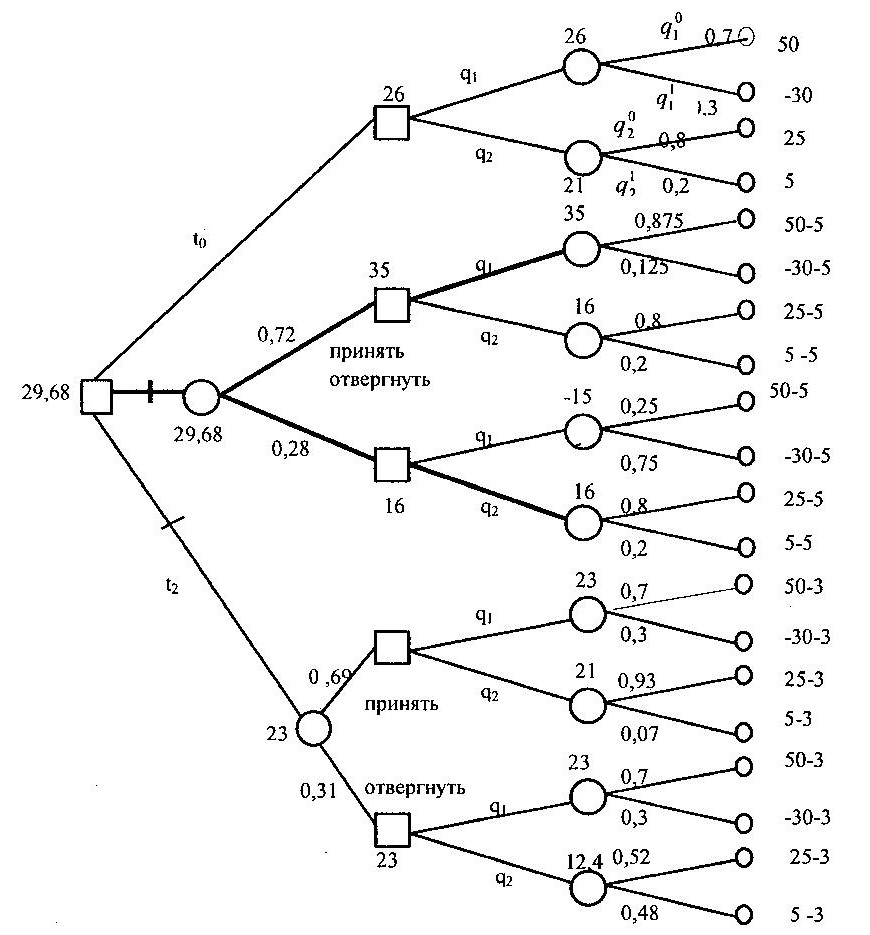
Рис. 5. Дерево решений с вероятностями на дугах и метками полезности на вершинах (Романов В.П. Интеллектуальные информационные системы в экономике //М., "Экзамен", 2007, стр. 109)