1.11. Критерий «тензорности». Примеры.  

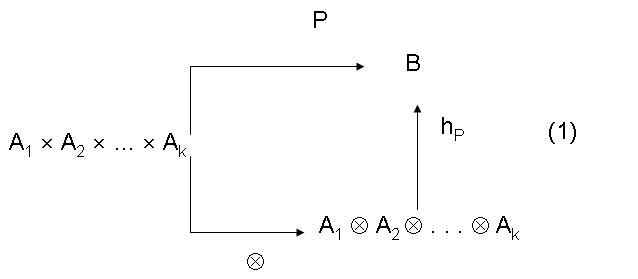
Одно из наиболее важных (по крайней мере с точки зрения алгебры) свойств тензорного произведения векторных пространств состоит в том, что с помощью этого произведения каждому полилинейному отображению канонически сопоставляется линейное. Действительно, рассмотрим диаграмму (1), где A₁, A₂, . . ., A_k – векторные пространства с одинаковым полем скаляров (а в остальном произвольные), P – некоторое полилинейное отображение множества A₁ ´ A₂ ´ . . . ´ A_k. В совокупности с каноническим отображением последнего в A₁ Ä A₂ Ä . . ., Ä A_k  P определяет отображение из  A₁ Ä A₂ Ä . . ., Ä A_k  в B, которое автоматически расширяется до отображения h_P всего пространства A₁ Ä A₂ Ä . . ., Ä A_k  в B , поскольку A₁ Ä A₂ Ä . . ., Ä A_k на множество значений отображения  Ä натянуто. Из полилинейности отображений Ä и P вытекает, что h_P – линейное отображение. Очевидно, кроме того, что диаграмма (1) коммутативна, т.е. P можно заменить суперпозицией отображений Ä и h_P.

Таким образом, для любой конечной системы A₁, A₂, . . ., A_k. В векторных пространств с одинаковым полем скаляров любое полилинейное отображение Р множества A₁ ´ A₂ ´ . . . ´ A_k в В порождает линейное отображение h_P пространства A₁ Ä A₂ Ä . . ., Ä A_k  в B, причем при заданных A₁ ´ A₂ ´ . . . ´ A_k. В отображение h_P зависит  только  от Р, и P(x₁, x₂, . . . , x_k) = h_P(x₁, x₂, . . . , x_k).

Перефразировка этого предложения может служить определением тензорного  произведения   A₁ Ä A₂ Ä . . ., Ä A_k  , вполне эквивалентным сформулированному ранее. В частности, и из этого определения немедленно вытекает, что естественными моделятензоров являются полилинейные отображения — для каждого тензора найдется (и притом не одно) полилинейное отображение, с которым этот тензор можно отождествить. Другими словами, математический или экономический объект может быть тензором лишь при условии, что задание этого объекта равносильно заданию какого-либо полилинейного отображения. В конечномерном случае это необходимое условие является и достаточным, представляя собой тем самым вполне определенный и достаточно удобный критерий для распознавания тензоров среди изучаемых объектов.

Рассмотрим несколько простых примеров, иллюстрирующих использование этого критерия.

I. Один из основных постулатов классической механики сплошной среды состоит в том, что взаимодействие вещества в любом „подобъеме" (v) с остальной массой среды вполне характеризуется полем s некоторого вектора на поверхности области (v). Фиксировав какую-либо точку среды, рассмотрим в качестве (v) элементарный тетраэдр с центром в этой точке и гранями, три из которых взаимно перпендикулярны (так что единичные векторы а₁, а₂, а₃ внешних нормалей к ним образуют ортонормированный базис). В этом случае из упомянутого постулата и условия равновесия (или сохранения импульса) вытекает s₁n₁ + s₂n₂ + s₃n₃ = s_n, где s₁, s₂, s₃, s_n — векторы поля s („векторы напряжения") на гранях тетраэдра, n₁, n₂, n₃  — составляющие орта n внешней нормали к грани с вектором напряжения s_v. Если х — произвольный вектор с направлением внешней нормали к этой грани, то n = x/|x| и (a₁ × x) s₁ + (a₂ × x) s₂ + (a₃ × x) s₃ = |x| s_n.  Очевидно, что отображение по закону x ® (a_i × x) s_i   есть линейная векторная функция вектора х Î E₃. Поэтому заданием векторов s₁, s₂, s₃, т. е. заданием „напряженного состояния" в данной точке среды, определяется некоторый двухвалентный тензор Т_s (тензор напряжения). С учетом „конструкции"  закона этой функции Т_s = aⁱs_i, откуда в свою очередь n × T_s = s_n.

II. Пусть u_ijk ( i, j, k = 1, 2, ... , n) —система из п³ чисел, характеризующая при заданном базисе е₁ е₂, ... , е_п пространства £_п некоторый „объект". Отображение по закону (х, у, z) ® u_ijkxⁱy^jz^k,  х = x = xⁱe_i, y = y^je_j, z = z^ke_k, представляет  собой трилинейную форму на E_n X E_п X E_n. Пусть, далее, е₁, е₂,..., е_п — какой-либо другой базис для E_п и п³ чисел u_ijk — компоненты исследуемого объекта в этом базисе. Отображение по   закону   (х, у, z) -> u_i’j’k’x^i’y^j’z^k’,    х = х^i’е_i’, у = у^j’е_j’, z = z^k’'e_k’, снова —трилинейная форма на E_n X E_п X E_n, однако не обязательно совпадающая с предыдущей. Любые две такие, порождаемые объектом рассматриваемого типа с заданием базисов для E_n, трилинейные формы на E_n X E_п X E_n совпадают тогда и только тогда, когда этот объект—(трехвалентный) тензор над E_n.

III. Рассмотрим какую-либо (в частности, не обязательно линейную) форму на E_n, т. е. функцию f: x ® f(x), x Î E_п со скалярными значениями. При фиксированном базисе для E_п функция f сводится к функции от п скалярных аргументов — компонент произвольного x Î E_п в данном базисе (или, если угодно, координат точки, радиус-вектором которой служит х). С учетом этого нетрудно проверить, что обычное определение дифференцируемости такой функции (по совокупности аргумен­тов) в некоторой точке равносильно определению, по которому f дифференцируема при х ® х₀, если для любого а Î E_п существует предел

                                             lim {(f(x_o + at) – f(x_o))/t: t®0},

причем   отображение   по правилу

                                                a ® lim {(f(x_o + at) – f(x_o))/t: t®0},   a Î E_п,

представляет собой линейную форму на E_п. Вследствие линейности этой форме соответствует вектор из E_п^* = E_п, т. е. одновалентный тензор над E_п, с которым ее можно отождествить. Этот вектор, обозначаемый обычно через f’(х_o) или Ñf(х₀), называется (полной) производной или градиентом функции f при х = х₀.

Учитывая, что по определению Ñf(х₀) (Ñf(х₀)) × a для каждого а Î E_n совпадает с указанным выше пределом, нетрудно установить связь с обычно определяемыми величинами. Так, для любого а с |а| = 1 скалярное произведение  (Ñf(х₀)) × a представляет собой то, что в классическом анализе принята называть „производной по направлению" (направлению вектора а). Соответственно при задании любого базиса е₁, е₂, ... , e_n Î E_n,  так что х = хⁱе_i и f сводится к функции на Rⁿ или Сⁿ, ¶f/¶xⁱ = (Ñf(х)) × e, откуда df = (¶f/¶xⁱ)dxⁱ = (Ñf(х)) × dx, dx = (dxⁱ) e_i.

Приведенное определение производной скалярной функции на E_n пригодно и для функций на А_п (с той лишь оговоркой, что в этом случае Ñf(х) — вектор из A_n*), а также, и это главное, естественным образом обобщается на случай функций, значения которых суть тензоры любой валентности.