К разделам сайта: Домой Примеры Теория индексов Банки Физика
Волновые особенности материального мира.
МАТРИЧНЫЙ КВАНТОВЫЙ СИСТЕМНЫЙ АНАЛИЗ
К ОСНОВАМ МАТРИЧНОЙ ЭКОНОМИКИ
1. Понятие квантования объекта
2. Многоэшелонированная структура дифференциации качества
3. Векторная интерпретация квантификации в гильбертовом пространстве.
4. Описание динамики состояния объекта в пространстве R3
5. Сравнение состояний. Понятие импульса.
6. Последовательность наблюдения качественных изменений.
7. Метрическая функция динамической задачи. Гамильтониан.
9. Интерпретация динамики гармоническим осциллятором
10. Фазовое представление наблюдаемой
11. Понятие потока
12. Оценки на схемах. Оператор плотности
13. Метрическое тождество в операторной форме
14. Оператор плотности и его селективные свойства
16. Оценки в локальных алгебрах
17. Оценки в полярном представлении
18. Производственные функции типа Кобба-Дугласа
19. Оператор конечного смещения
20. Понятие о напряжённом и деформированном состоянии системы
1. Понятие квантования объекта.
Понятие "квантование" будем использовать в том смысле, что некоторая экономическая величина фиксированного качества x может принимать дискретные числовые значения, например, x1, x2, …, xn, …, и между этими её значениями и величинами определённой числовой последовательности можно установить взаимно однозначное соответствие. В рассмотренном выше случае такой последовательностью является множество натуральных чисел N = {1, 2, …, n, …}. Примером квантования может служить задача построения структурированной схемы маркетинга некоторой организации.
Предположим, что целью некоторой организации служит сбыт продукции и для чистого сбыта продукции в стоимостном выражении введём обозначение x0. Как любая экономическая характеристика эта величина будет количественно w0 определённое качество Ψ0 (качественно Ψ0 определённое количество w0), т.е. x0 = w0Y0. Правую часть последнего равенства читаем как выручка w0 реализации Y0.
Проведём дезагрегацию сбыта. На первом уровне представим выручку в виде суммы факторов себестоимости x1 = w1Ψ1 и валовой прибыли x2 = w2Ψ2:
w0Y0 = w1Y1 + w2Y2.
Отсюда находим для исходной качественной характеристики деятельности организации математическое выражение в виде выпуклой линейной комбинации качественных характеристик первого уровня её дезагрегации
Y0 = l10Y1 + l20Y2, lk0 = wk / w0, k Î N1 = {1, 2}.
Получаем дихотомическую структуру с вершиной Y0 и двумя узлами Yk, k Î N1 нижнего уровня. Структурные элементы нижнего уровня связаны с вершиной схемы двумя отрезками - морфизмами [Y0, Y1] и [Y0, Y2], каждому из которых можно поставить во взаимно однозначное соответствие числовую характеристику l10 и l20, вес соответствующего отрезка в формировании единицы агрегатного качества Y0. Поскольку весовые коэффициенты положительны и в сумме равны единице, то их можно связать с вероятностью p10 и p20 присутствия каждого элемента в агрегатном качестве Y0 так, что p10 = l10 и p20 = l20.
Описание деятельности организации получится более детальным, если разбить, например, валовую прибыль на составляющие текущих расходов x3 = w3Y3 и чистую прибыль без учёта налогов x4 = w4Y4. Если на первом уровне дезагрегации нижний слой S1 состоял из элементов {Yk: k Î N1}, то на втором этапе агрегации имеем S2 = {Yk: k Î N2 = {1, 3, 4}}. При этом получаем структурное соотношение
Y2 = l32Y3 + l42Y4, lk2 = wk / w2, k Î N2 = {1, 3, 4},
l32 + l42 = 1.
При подстановке его в первое структурное равенство получаем выражение для целевой функции качества организации со второго уровня агрегации
Y0 = l10Y1 + l30Y3 + l40Y = l10Y1 + l20l32Y3 + l20l42Y4, l10 + l20l32 + l20l42 = 1.
Каждый элемент нижнего уровня с вершиной структуры связан единственным отрезком. Так как отрезок [Y0, Y3] пересекает второй уровень, то внутри него имеется элемент второго слоя. Это элемент Y2. Очевидно, что данный элемент принадлежит и второму отрезку [Y0, Y4]. При этом вес каждого из отрезков равен произведению весов отрезков их составляющих l30 = l20l32, l40 = l20l42.
Ещё более детальным получится описание, если, например, текущие расходы x3 разбить на более мелкие статьи: заработную плату с дополнительными выплатами x5 = w5Y5, арендную плату x6 = w6Y6, рекламу x7 = w7Y7, поставки x8 = w8Y8, страховки x9 = w9Y9, расходы на выплату процентов x10 = w10Y10, которые связаны с предыдущим уровнем агрегации отрезками [Y3, Yk], с соответствующими весовыми коэффициентами lk3, k Î N3(Y3) = {5, 6, 7, 8, 9, 10}. Целевая функция качества, равная единице сбыта товара, представляет выпуклую линейную комбинацию с коэффициентами в сумме равными единице
Y0 = l10Y1 + l40Y4 + l50Y5 + l60Y6 + l70Y7 + l80Y8 + l90Y9 + l100Y10.
Таким образом, сбыт товара x = x0, как и любая экономическая характеристика, "выступает, прежде всего, в виде произведения двух (и только двух) основных одинаково существенных взаимно дополнительных фундаментальных характеристик – внешней количественной интегральной характеристики w = w0 и внутренней качественной дифференциальной характеристики Y = Y0" [1, стр. 44]:
x = wY.
Декомпозиция единицы качества сбыта продукции представляет древовидную схему, содержащую два вида элементов: объекты Yk Î Y (здесь Y понимается как множество узлов схемы) и множество L отрезков jlk [Yk, Yl], соединяющих данные объекты, которую можно представить как абстрактный математический объект
K = (Y, L),
называемый категорией. Категории подобного древовидного типа относят к малым категориям, которые, в свою очередь, называются спектрами [2, стр. 67].
Отображение P: K -> P(K ), сохраняющее структуру категории, называется функтором. Очевидно, P(K ) = (P(Y ), P(L )). Функтор I: K -> I(K ), для которого при всех k, l Î N, если Yk Î Y и j lk Î L, то I(Yk) = Yl, I(j lk) = llk будет тождественным. Функтор W: K -> W(K ), для которого при всех k, l Î N, если Yk Î Y и jlk Î L, то W(Yk) = wk Î X, W(j lk) = plk Î H, где plk – вероятность связи элемента Yl структурной схемы категории K с её элементом Yk, снова будет категорией S = (X, P).
Величина wk =W(Yk) Î X определяет ожидаемую выручку от реализации продукции по представленной выше категорией K схеме маркетинга в узле Yk. Математическое ожидание от маркетинговой политики по предложенной схеме определяется выражением
w = W(Y0) = W(jk0)W(Yk) = (= SkÎN(n) W(jk0)W(Yk)) =
= p10 w1 + p40 w4 + p50 w5 + p60 w6 + p70 w7 + p80 w8 + p 0 w9 + p100 w10 = ò p dw
где для элементов последовательности квантования нижнего слоя схемы введено обозначение N(n) = Nn. Оценка
m(A) = òA p dm,
является линейным функционалом в пространстве интегрируемых функций
m(aA + bB) = am(A) + bm(B)
и показывает, что восприятие состояния x =A(K ) на фиксированной категории K зависит не только от его внешнего количественного восприятия xk = A(Yk ), k Î N(n), - состояния граничных элементов, но и от состояния его внутренней структуры pkl = A(jkl),k Î N(l), l = 1, 2, …,n, т.е. имеет место представление состояния объекта наблюдения
x = xF = Fx.
в виде произведения количественной характеристики на характеристику качественную. Обе эти характеристики могут изменяться со временем даже при неизменной его структуре K . Математически это свидетельствует о том, что от временного фактора зависит функтор A = A(t), т.е.
x(t) = A(t)(K ) = x(t)F(t).
Отсюда же следует, что качество объекта может зависеть от его количества и наоборот. Таким образом, в общем случае имеем
x = x(t, F), F = F(t, x).
Одним из таких примеров является наша потребительская корзина. Действительно, потребительская корзина со временем меняется. Она дифференцирована по товарам потребления, которые можно представить иерархической структурой. Так, например, в неё включаются продукты питания и товары для бытовых нужд, которые в дальнейшем можно дифференцировать по наборам продуктов и видам продуктов в этих наборах с дальнейшей их градацией вплоть до входящих в них ингредиентов. Аналогичная дифференциация может быть проведена и другой части корзины. При этом можно учесть, что качество товаров может меняться со временем.
Другим примером может служить размещение наших свободных денежных средств по банкам. Здесь нас интересует не только начисляемые в банках проценты по вкладам, но и фактическое состояние банков (их надёжность), которую мы можем оценить по доступным нам параметрам. Например, по публикуемым в печати показателям состояния банков по уровню капитала, активов, кредитов, вкладов населения, др. депозитов; по более детальной дифференциации в оценках банковской отчётности. Причём, расслоение объекта может теоретически быть бесконечным, т.е. Card N = n -> ¥ .
2. Многоэшелонированная структура дифференциации качества объекта.
Приведённые выше примеры показывают, что любой объект можно представить в виде связанной общим агрегатным свойством совокупности подобъектов, каждый из которых обладает своим, присущим только ему, индивидуальным свойством и такое расчленение носит иерархический характер, т.е. представимо многоэшелонированной структурой [3, Фиг. 2.9, стр. 68]. Каждый элемент (подобъект) этой структуры сам выступает в роли объекта, где подобъектами служат элементы основной структуры, входящие в орбиту [4, стр. 35] данного фиксированного элемента.
Предположим, что иерархическая структура состоит из n элементов xj, j Î N, имеет m слоёв Nk, k = 1, 2, …, m, и в орбиту элемента xs вышестоящего слоя Nk входят элементы xt, t Î Nl(xs), Nl –го слоя (k < l). Предполагаем, что для каждого слоя Nl имеет место расслоение Nl /Nk = {Nl(xs): s Î Nk}. Тогда метрическая функция F качества объекта x = xF при выделении слоя Nl при агрегации как граничного будет иметь вид
F = å kÎN(m) pkFk = å jÎN(l) p jFj , j < m,
где введены обозначения:
Fj = å kÎN(l, x(j)) pkj Fk ,
pkj = pk/pj, N(m) = Nm , N(l) = Nl, N(l, x(j)) = Nl(xj).
По той же структурной схеме агрегируется и дезагрегируется количественные характеристики:
x = å kÎN(m) pkxk = å jÎN(l) p jxj , xj = å kÎN(l, x(j)) pkj xk , j < m.
Таким образом, на фиксированной категорией K схеме объекта в состоянии x группа отображений G = {gkl: k, l Î M = {0, 1, 2, …, m}} расслаивает описание состояния объекта в стратифицированную схему, которая представляется градуированным пучком
0 →S0 →S1 → … → Sk → … → Sm → 0
в случае дезагрегации при описании состояния объекта и градуированным пучком
0 ← S0 ← S1 ← … ← Sk ← … ← Sm ← 0
в случае его агрегации. Каждый слой Sk является фактормножеством Sk /Sl, по разбиению Sl , l < k , и может служить граничным слоем.
Получаем гомоморфные градуированные пучки по расслоению множеств индексов N, системы качественных признаков F и системы количественных величин x, расслоения состояния объекта x по его стратифицированному описанию. При этом состояние объекта воспринимается системно. "Понимание системы возрастает при последовательном переходе от одной страты к другой: чем ниже мы опускаемся по иерархии, тем более детальным становится раскрытие системы, чем выше мы поднимаемся, тем яснее становится смысл и значение всей системы" [3, стр. 61]. В этой схеме каждый узел воспринимается как система со своей стратификацией.
3. Векторная интерпретация квантификации в гильбертовом пространстве.
Пусть элемент x некоторой структуры K принадлежит произвольной страте Sk её описания, а элементы xj , j Î Nl(x), другой страты Sl находятся с ним в бинарном отношении и множество Nl(x) линейно упорядочено (Nl(x) = 1, 2, …). Будем полагать, что данная система элементов полна, если на этой страте описания объекта нет других элементов, которые находились бы с элементом x в бинарном отношении. Состояние x = (xj| j Î N(x) = Nl(x)) элемента x, которое определяется состояниями xj элементов xj, назовём вектором. Пространство состояний X будем рассматривать в качестве линейного пространства данного фиксированного элемента, определив на объектах X операции тождественности состояний x = (xj| j Î N(x)) и y = (yj| j Î N(x)): x = y, xj = yj, j Î N(x), суммы: x + y = (xj + yj| j Î N(x)) и умножение на скалярную величину ax = (axj| j Î N(x)). На элементах пространства X определим скалярное произведение
m(x, y) = y*x = åjÎN(x)yj*xj.
Состояние структуры K как системы взаимосвязанных элементов определяется совокупностью состояний всех её элементов. На практике, состояния любой экономической системы можно описать подобным дискретным образом. Но, в ряде случаев представляется удобным описание её состояний в функциональных непрерывных или, даже, в кусочно-непрерывных пространствах. В этом случае скалярное произведение определим в виде
m(x, y) = òV(x)y(v)*x(v)dm .
При этом будем полагать, что индексируемое множество N может быть дискретным ограниченным, дискретным и неограниченным, ограниченным непрерывным и неограниченным, кусочно-непрерывным и частично дискретным и непрерывным.
4. Описание динамики состояния объекта в пространстве R3.
Рассмотрим множество объектов X. Будем полагать, что этому множеству принадлежит описание любого допустимого состояния x объекта наблюдения и всех состояний элементов его составляющих. Тогда это множество можно стратифицировать, полагая, что множеству X0 Ì X принадлежат все допустимые состояния на высшей страте описания состояния (вершины категории K), множеству X1 Ì X принадлежат элементы множества X0 и элементы описания всех возможных состояний объекта наблюдения с первого слоя их описания и т.д. Получаем, что одно и то же состояние объекта можно описать различным множеством факторов по стратифицированной схеме x Î X1 Ì X2 Ì ... Ì Xk Ì ... Ì X. Естественно, выбор страты Xk зависит от наблюдателя. При композиции происходит статистическое сжатие параметров описания состояния, становится яснее поведения объекта. Достаточно полную информацию о поведении объекта можно получить в двухмерном пространстве по наблюдениям за его количественными и качественными изменениями. Дадим экономическим характеристикам динамики объекта наглядную геометрическую интерпретацию в пространственно-временной структуре R4.
Рассмотрим динамику объекта в пространстве Xn его экономического описания. В пространственно-временной структуре эволюция состояния объекта происходит по некоторой непрерывной кривой. Пусть эта кривая описывается параметрическими уравнениями x = x(s), зависящими от натурального параметра кривой, которые будем полагать, по крайней мере, трижды дифференцируемы. Зафиксируем на кривой точку xo = x(0), в окрестности которой уравнения кривой разложим в ряд Тейлора и воспользуемся формулами Френе для выражения производных координат через геометрические параметры кривой, проецируя экономическое описание в геометрическое пространство R3. Для скорости кривой при удержании трёх главных членов разложения получим представление
v = e1 + ske2 + s2kce3.
Здесь ei , i = 1, 2, 3, векторы скорости, нормали и бинормали кривой в точке xo, соответственно, которые в окрестности этой точки определяют естественный трёхгранник Френе; k и c - кривизна и кручение кривой в окрестности данной точки - это геометрические параметры кривой, экономическое содержание которых заключается в том, что они характеризуют внутреннюю структурную перестройку, которая произошла при переходе объекта из состояния xo в состояние x = x(s), т. е. произошедшие качественные изменения. Такое агрегирование определяет проецирование пространства Xn в подпространство X3.
Нормированный вектор кривой
v = s 1e1 + s 2e2 + s 3e3.
будет единичным вектором скорости кривой в точке x = x(s) достаточно малой окрестности фиксированной точки xo, в котором коэффициенты si определяют доли вклада соответствующей составляющей, а их квадраты характеризуют вероятности обнаружения этого вклада.
Фиксировать положение направления вектора скорости в данной системе координат можно только двумя полярными углами q и j так, что его координатами будут величины
s 1 = cos q, s 2 = sin q cos j, s 3 = sin q sin j.
Здесь главный угол q, который характеризует кривизну кривой в окрестности точки xo, определяется поворотом e2 нормали (или касательной плоскости xoe1e3) к кривой в точке xo при переходе текущей точки в точку x, а угол j характеризует скручивание кривой и определяется поворотом вектора бинормали e3. Отсюда получаем, что переход организации из одного состояния в достаточно близкое другое её состояние можно интерпретировать галилеевыми преобразованиями координат.
5. Сравнение состояний. Понятие импульса.
Если объекты x = xF, y = hF качественно подобны, то из условия подобия x = ly следует количественное отношение x = lh, т.е
òA p dm =l òB p dm.
В этом случае сравнение объектов можно проводить по внешним агрегатным количественным признакам. Сложность сравнения появляется тогда, когда возникает потребность в сравнении разнокачественных объектов, т.е. объектов вида x = xF, y = hY, в том числе объектов с переменной структурой [4, стр.35], когда Y = Y(K ), F = F(K '), где K и K ' различны.
Рассмотрим множество объектов X, которые сравниваются с объектами множества Y. Объекты y множества Y будем называть эталонами. Основное назначение эталона y Î Y обусловим тем, что содержащаяся в нём информация служит для оценки содержания аналогичной информации в объектах x множества X. Для сравнения выбранного объекта с эталоном необходимо построить ту или иную функцию предпочтения m, которая даёт оценку информации, в единицах её содержания в эталоне. Данную функцию определим как меру сходства объекта с эталоном. Обычно меру строят на бинарных отношениях множества X´Y с её значениями на множестве действительных чисел R. Простейшая функция предпочтения, которая обращает пространство X в линейное пространство со стандартной топологией, индуцируется любой евклидовой метрикой, вводимой на X´Y положительно определённой симметричной билинейной формой m: Z = X´Y -> R. Эту функцию представим в виде
m(z) = f(y)(x) = y*x, z Î Z,
где отображение f: Y -> Y* осуществляет преобразование пространства эталонов в сопряжённое ему векторное пространство Y*. Учитывая симметрию метрической функции, введём функцию h: X → X* такую, что имеет место отношение
m* = m(z*) = h(x)(y) = x*y, z* = (y, x) = -z Î Z*,
где x* Î X*, и продолжим эту функцию на пространства X´X* и Y´Y*. В силу симметрии заключаем, что справедливо равенство m* = m, которое даёт возможность нормировать пространства X и Y
s(x) = m1/2(x, x), s(y) = m1/2(y, y)
и, воспользовавшись неравенством Коши-Буняковского, получить основное метрическое тожество на пространстве бинарных отношений X´Y, тождество Пифагора,
s2 = m2 + n2
где введено обозначение s = s(z) = s(x)s(y).
Учитывая, что из подобия x = ly получаем отношение s(x) = ls(y), заключаем, что функционал n = ± G1/2(z), где G(z) = G(x, y) – определитель Грама, построенный на векторах x и y, определяет меру отличия объекта наблюдения x от фиксированного эталона y.
В большинстве задач экономической практики в качестве эталонов берут элементы множества X. В этом случае Y Ì X и метрическая функция m обращает множество X в многообразие римановой структуры, которая позволяет выбором евклидовой структуры в окрестности эталона сравнивать, путём суммирования малых длин векторов, отрезки траекторий и направления эволюций объектов в этой окрестности.
Метрическая функция n дуальна метрической функции m. Если последняя является мерой сходства объектов, то функция n служит мерой их расхождения. Очевидно, в оценках можно с равным успехом использовать и ту и другую по мере удобства. Если мера сходства определяется скалярным произведением, то мера расхождения определяется кососкалярным произведением и, точно так же, как мера сходства задаёт на данном многообразии риманову структуру, кососкалянное произведение определяет на этом многообразии симплектическую структуру. Симплектическая структура позволяет измерять "площади" ориентированных двумерных поверхностей, суммируя поверхности малых параллелограммов, что даёт возможность проводить анализ в пространстве возможностей эволюции, используя его пространственные характеристики такие, например, как кривизны пространства в окрестности эталона и т.п. В метрическом тождестве на тернарном отношении (x, y, e), где e – единичный элемент пространства эталонов, реализовано гегелевское диалектическое единство качества, количества и меры.
Введём новую комплексную метрическую функцию, которая даёт полное описание состояния объекта
F = F(z) = m(z) - i n(z)= sU, U = e j,
где введены обозначения
j = Arth e, e = -iv/m,
и определим комплексно сопряжённую ей функцию
F* = sU* = m* - i n* =`F = F(z*), U* = e -j,
так, что отношение
F*F = s 2,
в развёрнутом виде представляет равенство
F(y, x)F(x, y) = D(x)D(y),
которое утверждает, что если состояния объекта наблюдения и эталона независимы и описаны полным образом, то оценка D системы z = (x, y) равна произведению оценок состояния каждой из них и это соотношение сохраняется и в будущие моменты времени
D(z) = F*(t, z)F(t, z), z = z(t).
Новая метрическая функция представляет собой единство количественной меры, характеризуемой её модулем s, и меры качества, которая определяется унитарным оператором U. Оператор качества даёт оценку структурных преобразований при возможном переходе наблюдаемого объекта из одного состояния x в другое y возможное состояние, при этом предполагается его гипотетически возможное возвращение в исходное состояние не меняет первоначального состояния системы z.
Модуль
s = m(1 - e2)1/2
доставляет оценку агрегатных значений количественных величин сравниваемых объектов, а аргумент
j = -iq/h
выражается через масштабированную величиной h характеристику структурных сдвигов
q = h arctg(n/m).
и позволяет оценивать качественные отклонения объекта наблюдения от эталона путём отображения с экспоненциальной шкалы на линейную шкалу.
Введённая здесь постоянная величина h играет роль масштабного метрического коэффициента при сопоставлении качественного сходства и различия объекта с эталоном. При малом качественном различии имеем приближённое равенство
q » hn / m.,
из которого следует, что эта постоянная является соизмерителем метрических пространств (Z, m) и (Z, n), которые определяют риманову и симплектическую структуры на пространстве возможных состояний X´Y.
Если рассматривать наблюдение как процесс перехода объекта из одного состояния в другое, то когда в переходном процессе не происходят качественные сдвиги, величина q = 0 при этом, унитарный оператор обращается в тождественный. С ростом качественных сдвигов данный угловой показатель монотонно возрастает. Таким образом, с ростом качественного различия абсолютная величина аргумента j унитарного оператора возрастает. Но, для перевода объекта из одного состояния в другое необходимо приложить некоторое усилие, импульс. Следовательно, оператор U = U(j) характеризует ту составляющую равнодействующей импульса, которая приводит в рассматриваемом переходном процессе к качественным изменениям объекта.
Если метрическую функцию представить в виде нелинейного среднего [5]
F = e –M/h, M = - h(j + ln s ),
то сопряжённая функция принимает вид
F* = e –M*/h, M* = - h(- j + ln s ).
6. Последовательность наблюдения качественных изменений.
Как правило, наблюдения в социальной и экономической сфере носят дискретный характер, т.е. проводятся в разные моменты времени.
Предположим, что объект x наблюдается на некотором временном интервале T в моменты времени t1 и t2. Тогда в данные моменты мы наблюдаем два соответствующих состояния x1 = x(t1) и x2 = x(t2) объекта. Исходное предположение о наблюдении содержит гипотезу о зависимости состояния объекта наблюдения от времени. Запишем эти наблюдения в виде следующей линейной комбинации
x = ax1 + bx2, a + b = 1.
Если a = 1, то наблюдается событие x1 в момент времени t1. Если же a = 0, то b = 1 и наблюдается событие x2 в момент времени t2. Здесь коэффициенты линейной комбинации можно рассматривать в качестве вероятностей наблюдения соответствующих состояний. При этом, преобразования
a = a(t) = (t – t1)/(t2 – t1), (t = (t2 – t1)a + t1),
устанавливают взаимно однозначные соответствия между точками временного отрезка [t1, t2] наблюдениями и единичным интервалом [0, 1].
7. Метрическая функция динамической задачи. Гамильтониан.
Как было отмечено выше, метрическая функция F = sU полностью описывает поведение наблюдаемого объекта с количественной и качественной стороны по агрегатным показателям, т.е. знание поведения этой функции до некоторого момента времени можно не только определить все её характеристики в данный момент, но и определить её поведение в будущем. В общем случае, метрическая функция не только может зависеть от поведения наблюдаемого объекта x = x(t) и поведения эталона y = y(t), но и зависеть от времени явно, F = F(t, x, y). Это обуславливает то, что её изменение связано линейным оператором от самой функции. Действительно, частная производная метрической функции по временному фактору определяется волновым уравнением
h ¶ tF = -HF,
где оператор, стоящий в правой части уравнения является гамильтонианом и определяется соотношением
¶ tM = H.
Полагая, что гамильтониан явно не зависит от времени H = iE = ¶ tM = const, найдём
F = f(z)e –iEt/h.
Направление наискорейшего роста функции F определяется её градиентом и пропорционально приложенному к объектам, находящимся в данном бинарном отношении, равнодействующему импульсу p*. Приходим к соотношению
ÑF /F = Ñf / f = ip*.
Отсюда находим значение функции
j = C e i p*z
и окончательное значение для метрической функции оценки бинарного состояния в произвольном узле схемы K
F = C e -i(Et – p*z)/h.
Для граничного узла k Î N на K будем иметь
Fk = Ck exp(-i(Ekt – pk*zk)/hk),
а для её вершины получаем выражение
F0 = å k Î N ak exp(-i(Ekt – pk*zk)/hk), ak = pk0 Ck.
В 1924 году французский физик Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм в физическом мире носит универсальный характер. Этот факт остаётся справедливым и для материального мира как образа реального мира в сознании человека и сознания человечества в целом. В соответствие с этой гипотезой метрическую функцию объекта будем рассматривать в виде композиции плоских волн де Бройля
xk(t, z) = ak exp(-i(Ekt – pk*zk)/hk)
исходящих от его граничных элементов, k Î Nn, где амплитуда ak каждой волны зависит от вероятности наблюдения соответствующего граничного элемента в агрегатном состоянии, а её энергия Ek и импульс pk связаны с круговой частотой wk и длиной волны lk соотношениями
Ek = hkwk, pk = 2phk / lk.
В объекте наблюдения, в его агрегатном свойстве, каждый граничный элемент представлен волновым процессом с частотой wk = Ek / hk и длиной волны lk = 2phk / Fk.
Скорость распространения соответствующей волны можно определить, если зафиксировать некоторую её фазу Ekt - pk* zk = const и продифференцировать её по параметру t
vk = dzk / dt = ( pk*)-1Ek.
Из предыдущего вывода метрической функции следует, что она является комплексной, т.е. имеет вид суммы действительной и мнимой частей. Поэтому экономический смысл имеет не сама функция, а её модуль и аргумент. Из волнового уравнения видим, что метрическая функция определяется с точностью до постоянного множителя. Её можно нормировать так, чтобы модуль был равен единице. Тогда отклонение от единицы квадрата модуля D = |F |2 = F*F можно рассматривать в качестве вероятности обнаружения объекта наблюдения в состоянии x относительно состояния y эталона в их бинарном отношении z = (x, y). Отсюда получаем выражение
dD = |F|2dz = F*F dz,
из которого находим вероятностную оценку отклонения состояния объекта от эталона в области наблюдения A Í X´Y [6, (2.1)]
D(t, A) = òA F*F dz £ D(t, X´Y) = 1.
Если разложить целевую функцию системы по её структурным элементам F = akFk, а ей сопряжённую функцию записать в виде F* = (ak)*(Fk)* = akFk, то из условия её нормировки получим разложение единицы
1 = å kÎN akak = å kÎN ak òFkF dz,
из которого находим
ak = òFkF dz, òFkFl dz = d kl.
При возмущении границы объекта оператором W целевая функция изменяется и принимает значение Y = WF. Учитывая выражение Y* = F*W* для её сопряжённого значения, получаем, что оценке состояния системы можно поставить в соответствие величину
w = ò F*WF dz,
равную среднему значению оператора W = W*W .
Рассмотрим некоторый экономический объект, предположим, что нашим объектом является предприятие. Пусть предприятие выпускает продукцию в количестве q и реализует её по цене p. Выручку предприятия оценим величиной T = p*q и определим её как "живая энергия" предприятия. Величиной V оценим упущенные потенциальные возможности предприятия и величину E = T + V назовём полной энергией. В соответствии с теоретической механикой введём двойственную функцию L = T – V, функцию Лагранжа, и составим выражение
EL = T2 – V2.
Приходим к основному метрическому тождеству, в котором s2 = EL, m = T, n = -iV, Отсюда получаем, что F = L, F* = E.
Состояния, в которых полная энергия принимает определённое значение, называются стационарными. В стационарных состояниях значение энергии является собственной функцией гамильтониана, т.е. HF = EF и волновое уравнение принимает вид
ih ¶ tF = EF.
Ясно, что выпуск продукции является функцией её цены и в первом приближении можно ограничиться линейными членами q = Ap. Для живой энергии получаем выражение T = p*Ap. Цена на продукцию служит импульсом к её выпуску, который, в свою очередь пропорционален градиенту. Эту зависимость запишем выражением pa = -ihÑa . Полагая для простоты, что оператор живой энергии имеет диагональный вид A = 1/2ma I. где I – тождественный оператор, получаем следующее уравнение
ih ¶ tF = (-h2/2 å a Da/ma + U)F.
Это уравнение для агрегатной метрической функции объекта, находящегося во внешнем поле социальной активности, принимает вид
ih¶ tFo = -h2/2m DFo + VFo.
Для стационарного состояния имеем
h2/2m DFo + (E - V)Fo = 0.
Для предприятия с живой энергией T = p*q = g p2, эволюция которого протекает в отсутствии внешних воздействий (E = T, V = 0) в направлении координатной оси, отвечающей выпуску продукции q, данное уравнение, полученное Шредингером в 1926 г., принимает вид
ih ¶ tF = -g h2 ¶ q2F.
Его решением является волновая функция
F(t, q) = Aexp(-i(Et – p*q)/h),
которая описывает плоскою волну де Бройля. Данный факт даёт возможность утверждать, что уравнение Шредингера и в общем случае описывает волновой процесс.
В подобной задаче к уравнению Шредингера можно придти и другим методом, используя, например, методы матричной квантовой механики [7, стр. 55].
9. Интерпретация динамики гармоническим осциллятором.
В рамках линейной модели построим оценку фактического состояния системы (q, p) (q – вектор реализации продукции, импульсом которой служит вектор цен p) относительно расчётного (qo, po). Определим фактический D(q) = p*q и расчётный D(qo) = po*qo доход от реализации и представим гамильтониан H бинарного отношения (q, qo) в виде
H = ½ D(q)/D(qo).
Для этого построим метрическую функцию сходства m = qo*q и, принимая линейную зависимость q = Ap реализации продукции от её цены, запишем её квадрат в виде квадрата новой функции цены m2/D2(q0) = P*P = P2, где введено обозначение: P = po*Ao*Ap/D2(q0). Обращаясь к основному метрическому тождеству, второе слагаемое в его правой части представим квадратом некоторой функции параметра реализации: n2/D2(q0) = G(q, qo)/D2(q0) = Q2(q). Приходим к следующему представлению гамильтониана формулой (3, 3) работы [7]
H =½ ( P2(p) +Q2(q)) = F*F +E.
Здесь F - новая метрическая функция. Её значение определим в виде
F = (Q + iP)/21/2,
а отвечающее ей сопряжённое выражение – в виде
F* = (Q - iP)/21/2.
Тогда будут справедливы коммутационные соотношения
FF* - F*F = 2E, PQ – QP = 2iE.
Учитывая представления
2H = P2 + Q2 = (P – iQ)(P + iQ) +2E = P2 + Q2 +i(PQ – QP) + 2E
и используя перестановочное соотношение Гейзенберга [7, стр. 53]
QP –PQ = ihQ',
для операторов P и Q, найдём, что
Q2 = Q2 + hQ' + 2E.
Если ввести подстановкой
Q = h (ln Ψ)'
новую метрическую функцию Ψ, то приходим к равенству
Q2 = h2Ψ''/Ψ + 2E,
из которого относительно вспомогательной функции Ψ получаем уравнение Шредингера
h2Ψ'' + (2E – Q2)Ψ = 0.
В случае, когда процесс фактической реализации товара качественно подобен расчётным показателям, Q = 0 и индекс товарооборота Ipq = D(q)/D(qo) равен квадрату индекса физического объёма продаж Iq = m(q, qo)/D(qo). При отклонении качества от расчётного величина 2E – Q2 = 2E становится положительной.
Если ввести обозначение
w2 = 2E/h2,
то приходим к уравнению для простейшего гармонического осциллятора
Y'' + w2Y = 0.
А с учётом действительности искомого функционала, общее решение этого уравнения принимает вид плоской стоячей волны
Y = C cos wq.
Здесь величина w является циклической частотой колебаний.
Обычно, если за основную метрическую функцию берётся функция F = (P + iQ)/21/2, то полагается E = ½; если берётся функция F = (P - iQ)/21/2, то E полагается равным -1/2. Таким образом, величина E является собственным значением гамильтониана рассматриваемой задачи и характеризует спин функций F и F*. С учётом того, что эта величина в последнем случае является наименьшим собственным значением оператора H и Q2 < 1 заключаем, что величина 2E – Q2 положительна и меньше единицы. Полагая
k2 = (2E - Q2)/h2,
приходим к заключению, что и в общем случае рассматриваемый процесс описывается простейшим гармоническим осциллятором
Y'' + k2Y = 0
с циклической частотой k.
Из соотношения
D(q) = 2HD(q0)
заключаем, что собственное значение H = E = ½ даёт минимальное кратное единице измерения значение величины дохода
D(q) = D(q0),
и в выбранных единицах измерения значение дохода определяется величиной
D(q) = lΨ(q0),
где величина l = ½ является наименьшим собственным значением оператора H = ½ (P2 + Q2), собственные значения которого определяются формулой: lj = ½ (2j – 1), j Î N = {1, 2, …}, а Ψ – некоторая надлежащим образом нормированная функция качества.
10. Фазовое представление наблюдаемой и среднеквадратичная флуктуация.
Принцип неопределённости Гейзенберга
Пусть Q - наблюдаемая величина метрического пространства (X, m) элементов фиксированного качества Ψ. Тогда объект можно определить в виде x = QΨ Î X. Если наблюдаемая является тензором валентности n = Card X, то Ψ характеризует некоторую карту в этом пространстве, т.е. имеет ту же размерность. Предположим, что наблюдаемая меняется и меняется под действием импульса P, т.е. состояние объекта характеризуется бинарным соответствием (Q, P). Пространство импульсов определим как сопряжённое пространство X*, объектами которого являются сопряжённые элементы y* = = Ψ*P*, полагая, что Ψ** = Ψ. Величину Q определим в качестве обобщённой координаты состояния объекта, а величину P – как обобщённый импульс данного состояния. Пространство допустимых состояний C = (Q, P) назовём фазовым пространством Z. Пространство его обобщённых координат определим как конфигурационное пространство. Состояние объекта описывается фазовой точкой z = CΨ в фазовом пространстве Z. Размерность фазового пространства равна 2n.
Будем представлять это состояние в комплексной форме z = x +iy = (Q + iP)Ψ и меру m с конфигурационного пространства расширим на всё фазовое пространство, т.е. будем фазовое пространство рассматривать как метрическое пространство (Z, m), где среднее значение c наблюдаемой C определяется оценкой
c = m(z, Ψ) = Ψ*CΨ = q + ip,
где q = m(x, Ψ), p = m(y, Ψ) – средние значения обобщённой координаты и обобщённого импульса, соответственно. Очевидно, "фазовое пространство ничего общего не имеет с реальным пространством и является лишь геометрической схемой, с помощью которой законы изменения состояния системы могут быть сформулированы на геометрическом языке". В фазовом пространстве состояние изображается фазовой точкой, а его изменение – фазовой траекторией. Фазовую траекторию оценим уравнением c = c(t), а фазовое отклонение от неё наблюдаемой - дисперсией
D(C – c) = Ψ*((C – c)*(C – c))Ψ.
Рассмотрим наблюдаемую в фазовом пространстве с корректирующим параметром a. Представим её в виде С(a) = Q + iaP. Её средней будет величина c(a) = q + iap. Дисперсионная оценка отклонения фазовой переменной от её среднего значения легко преобразуется к виду
D(C(a) – c(a)) = D(P – p)a2 +iaΨ*(QP – PQ)Ψ + D(Q – q).
Учитывая неотрицательность дисперсии и принимая постулируемое Гейзенбергом коммуникационное соотношение
QP – PQ = ih,
относительно корректирующего параметра a получаем квадратичное неравенство
D(P – p)a2 - ha + D(Q – q)³ 0,
из которого следует, что произведение среднеквадратических оценок флуктуаций обобщённой координаты и импульса должно быть не меньше некоторого фиксированного числа h/2, т.е.
s(Q – q)s(P – p) ³ h/2.
В основном состоянии простейшего гармонического осциллятора это неравенство достигает своего абсолютного минимума.
11. Понятие потока.
Рассмотрим некоторый объект, которым может являться, торговая сеть, предприятие и т.п., для которого типичны функции снабжения (товаром, сырьём) и реализации конечной продукции. Представим деятельность объекта по переработке поступающих ресурсов в конечную продукцию в виде "чёрного ящика", а саму схему объекта представим в виде объединённой одной вершиной – "чёрным ящиком", прямого и обратного спектров. Граничные элементы прямого спектра являются входом ресурсов из внешней среды и являются одним типом граничных элементов объекта. Граничные элементы обратного спектра служат граничными элементами второго типа для объекта, посредством данных элементов объект решает задачу реализации своей продукции в окружающую среду. Объект в целом определим как объем V ограниченный поверхностью S. Если предприятие функционирует, то имеет место отличная от нуля оценка
P = ò V |F |2dV.
Если же эта оценка меняется со временем, то это свидетельствует о наличии потока
dП = dP/dt
ресурсов через граничные элементы – поверхность S, что и ведёт к изменению оценки деятельности предприятия.
Естественно полагать, что поток распределён по всей граничной поверхности S. Для его оценки введём показатель j плотности потока, определив его соотношением
П = - ∲S j dS,
Применяя к правой части данного соотношения теорему Остроградского, будем иметь
П = - òV div j dV.
Следовательно,
òV (¶ t |F|2 + div j) dV = 0
и
¶ t |F|2 + div j = 0.
Но,
¶ t |F|2 = ¶ t (F*F) = ¶ t (F*) F + F* ¶ t (F).
Если метрическая функция F удовлетворяет уравнению Шредингера
ih ¶ t F = - ghDF +UF,
то сопряжённая ей функция F* удовлетворяет уравнению
-ih ¶ t F* = - ghDF* + F*U.
Здесь использовано то, что живая энергия пропорциональна квадрату импульса T = gp2/h, а импульс пропорционален градиенту p = -ihÑ, т.е. T = -ghÑ 2 = -ghD.
Умножим слева первое уравнение на функцию F*, второе уравнение - справа на функцию F, и из первого полученного соотношение вычтем второе, приходим к равенству
ih ¶ t |F |2 = -gh((F*DF - (DF*)F).
Если теперь воспользоваться равенствами векторного анализа
div(F*ÑF) = ÑF*ÑF + F*DF, div((ÑF*)F) = ÑF*ÑF + (DF*)F,
то получим
F*DF - (DF*)F = div(F*ÑF - (ÑF*)F),
или
ih ¶ t |F |2 + gh div(F*ÑF - (ÑF*)F) = 0.
Окончательно приходим к соотношению
¶ t |F |2 + ig div((ÑF*)F - F*ÑF) = 0,
из которого находим выражение для вектора плотности потока
j = ig ((ÑF*)F - F*ÑF).
Пусть Q – линейный оператор, действие QF которого на метрическую функцию F определяет ресурсы, распределённые на граничном слое в задаче снабжения предприятия, а величина q = F*QF даёт агрегатную оценку этих ресурсов (возможно, в стоимостном выражении). Тогда величины q и jq = Qj = ig ((ÑF*)QF - F*Ñ(QF)) определяют, соответственно, оценки количества ресурсов и плотность потока движения этих ресурсов к предприятию по схеме снабжения, а уравнение
¶ t q + div jq = 0
служит оценкой непрерывности этого потока и является аналогом уравнения непрерывности в механике сплошных сред. Совершенно аналогичной выглядит задача интерпретации на диаграмме маркетинга. Задачи снабжения и маркетинга можно объединить в одной диаграмме (дерево = корни + ветви). Более того, в этой диаграмме можно дифференцировать по качественным признакам само производство продукции на предприятии и рассмотреть представление о деятельности предприятия на сложной схеме типа нейронной сети [8].
Пусть переход объекта из состояния x в состояние y характеризуется качественными преобразованиями и метрическая функция F = F(x, y) определяется в виде плоской волны де Бройля
F = Aexp(-i(Et – px)/h).
Найдём основные характеристические параметры данного перехода.
В общем случае метрическая функция имеет вид F = u – iv = s exp(-iq/h) и удовлетворяет уравнению ih¶tF = HF. Очевидно, при сравнении состояние x по качественным признакам должно быть близко к состоянию y (x » ay), т.е. u >>v и s » u¸а поскольку рассматриваются качественные преобразования, то можно предполагать, что относительная величина оценки s во времени меняется медленно по сравнению с качественными изменениями. Тогда F*F = s2 = u2, т.е. s = u и H = E = ¶ t q = wh. Найдём отличные от нуля компоненты градиентов
ÑF = ¶ x F = ipF/h, ÑF* = ¶ x F* = -ipF*/h
и определим соответствующую составляющую вектора плотности потока
jx = 2gp/h F*F = 2gpu2/h = 2gku2.
Здесь волновой вектор k = p/h задаёт направление распространение волны структурных преобразований при переходе из одного состояния в другое. С помощью модуля волнового вектора, волнового числа k, находим длину волны l = 2p/k .
В силу уравнения Шредингера метрическая функция определяется с точностью до постоянного множителя. Это объясняет тот факт, что при сопоставлении одного состояния с другим можно переходить от одной единицы измерения к другой. Нормируя метрическую функцию так, чтобы jx = a2, находим скорость структурных преобразований vx = a2/u2 и меру инерции объекта по отношению этих преобразований m = pu2/a2 .
12. Оценки на схемах одинаковой структуры. Оператор плотности.
Вернёмся к интерпретации эволюции в геометрическом пространстве R3. В этом пространстве динамика объекта определяется непрерывной кривой, а в момент времени t её характеризует касательный вектор v скорости эволюции (п. 3), который задаётся тремя составляющими – его проекциями на оси координат пространства R3. Интегральная оценка динамики
w = v*Wv
является функция временного параметра. Фиксируя лишь направление эволюции в каждой точке кривой, можно следить за динамикой структурных сдвигов. В этом случае фиксирование направления v вектора двумя полярными углами q и j наталкивает на мысль, что каждому элементу v пространства можно поставить в соответствие собственный вектор a+ второго порядка некоторого оператора sq,j , отвечающий собственному значению +1. Ему противоположным вектором будет ортонормированный вектор a-, равный собственному вектору этого оператора, соответствующему собственному значению -1. Таким оператором, в данном случае, является тензор второго ранга, который, записанный в обозначениях MATLAB, имеет вид
sq,j = [cos q e-ij sin q; e ij sin q -cos q].
Собственными векторами этого тензора, соответствующие собственным значениям 1 и -1, будут векторы-столбцы
a+ = [cos q /2: eij sin q /2], a_ = [e -ij sin q /2: -cos q /2],
а эрмитово сопряжённым вектором вектору a+ будет вектор-строка
a+* = [cos q /2 e -ij sin q /2].
Каждому базисному вектору естественного трёхгранника Френе отвечает свой тензор. Так, касательному вектору e1 соответствует тензор s1 = s0,0 = [1 0;0 -1]; вектору нормали e2 - тензор s2 = Tr/2,0 = [0 1;1 0]; вектору бинормали e3 - тензор s3 = Tr/2,p/2, = [0 i;-i 0]. Разложению
v = s 1e1 + s 2e2 + s 3e3
отвечает эквивалентное представление
s = sq,j = s 1s1 + s 2s2 + s 3s3.
Если связать параметр кривой с временным фактором, то можно утверждать, что вероятность обнаружить объект в состоянии v, если он в начальный момент находился в состоянии vo, равна
1 = ||v||2 = v*v = a+*sq,ja+ =`sq,j ,
где `sq,j - среднее значение оператора sq,j по мере a+ . Таким образом, заключаем, что оценка нормы вектора v связывается с оценкой соответствующего ему тензора s. Тензор s = sq,j называется оператором плотности [9]. Если же среднее значение оператора s взять за его норму ||s|| в соответствующем пространстве, то приходим к равенству
||v|| = ||s ||.
Базисные тензоры si оператора плотности называются матрицами Паули. Вместе с тождественным тензором I они обладают свойствами
sisj + sjsi = 2dijI, sisj - s jsi = 2i(-1)ask ,
где i, j, k принимают значения из последовательности 1, 2, 3; a = a(i, j, k) - значение их перестановки, a(1, 2, 3) = 1. Оператор s = 1/2s называется спином. В данном случае норма спина равна 1/2, а сам он определяет некоторую ориентацию в заданном базисе пространства R3.
Чтобы понять такое явление как спин можно обратиться к следующей задаче социального содержания.
Все мы живём в некотором поле социальной активности, имеющем определённую направленность в исторически сформированных ценностях, которые формируют социальный базис. Это поле требует от каждого из нас определённой ориентации, определённой социальной ответственности в данном базисе. Но, в силу различия способностей и возможностей каждого из нас, как правило, не удаётся выдержать должную ориентацию, появляется отклонение. У каждого индивида появляется своё отклонение, а у социума, как среднее, своё. Эти отклонения и называются спином. При ориентации базисного тензора по направлению s1 спин показывает ориентацию объекта (субъекта) относительно заданного направления в исходном базисе. Возможность исследования состояния организации с помощью оператора плотности впервые было отмечено Ландау (1927).
13. Метрическое тождество в операторной форме.
Записанное для состояний x = AY и y = BY метрическое тождество принимает вид
x*Py = x*Qy + x*Ry,
где операторы плотности P, Q, R удовлетворяют свойствам:
P = AYY*B* = Q+, Q = BYY*A* = P*, R = P - Q = Q* - Q = - R*,
из которых следует, что все три входящие в метрическое равенство выражения определяются заданием только одного оператора плотности, оператора Q или оператора P. При условии полноты YY* = I метрического пространства состояний P = AB* Действительно, если пространство X банахово и x, y Î X, то будет построен оператор P как плотность произведения квадратов их норм, и, следовательно, можно построить операторы сходства Q и расхождения R. Более того, для следа оператора P получаем равенство
Tr P = µ.
Пусть x, y Î X и состояние y является эталоном для оценки состояния x. Эту оценку запишем в виде µ = µ(x, y) = y*x. Тогда
µ2 = y*M(x, y)x,
где для оператора плотности введено обозначение
M(x, y) = xy*.
Естественно, что µ = Tr M .
Левую часть основного метрического тождества можно представить в виде
s2 = y*M(y, x)x
и в общем случае s ¹ µ, то M(y, x) ¹ M(x, y).
Поскольку имеет место равенство
M*(y, x) = M(x, y),
то из основного метрического тождества находим
R(x, y) = M(y, x) - M(x, y) = - R(y, x).
Отсюда при качественном подобии состояний x = ly получаем соотношения
M(y, x) = M(x, y) = lM(x, x) = lM(x).
Обозначение
M(x, x) = M(x)
принимается, когда в качестве измерительного эталона выступает само состояние. В этом случае
µ(x,x) = Dx = Tr M(x)
и
M*(x) = M(x).
При нормировании состояния x имеем Tr M(x) = 1 и x определяется как чистое состояние. Аналогичное выражение получаем для меры D(x, y) = s2 (x, y) = DxDy:
D = Tr (M(x)M(y)) = Tr M(x) Tr M(y).
При x = AY среднее значение наблюдаемой A в состоянии, которое описывается оператором M = M(Y), будет равно
a = Tr (MA) = Tr (AM).
Для чистого состояния y = Y оператор M удовлетворяет равенству
M2 = M.
Из которого следует, что все его собственные значения равны либо нулю, либо единице.
Но, из условия, что след равен единице, заключаем, что единице равно только одно его собственное значение. Так как действие оператора M на произвольный элемент x Î X есть разложение этого элемента по собственным функциям ej (свойствам) оператора M
Mx = xiei
и
M(ek)ej = dkjej,
то из соотношения
M(ej)x = xjej
заключаем, что действие оператора M(ej) на произвольный элемент x Î X даёт оценку j-го свойства в данном элементе, отделяя это свойство в нём от влияния всех остальных его свойств. Следовательно, оператор M(ek) действует как проектор множества X на числовую ось, направляющим вектором которой является собственный элемент ej этого оператора.
В качестве примера сравним расчётное состояние y с фактическим состоянием x на примере планирования эволюции некоторого объекта. Предположим, что на основании прошлого опыта прогнозируемое состояние определено вектором y. Фактически же наблюдаем состояние x. Естественно в основу метрики для сопоставления векторов положить скалярное произведение µ = y*x. Поскольку задача сопоставление амплитуд sx и sy данных векторов решается достаточно просто, то возникает проблема описания их ориентаций, т.е. задача сравнения направлений их масштабных векторов, которые и примем за x и y, полагая sx = sy = 1.
Задачу интерпретируем следующим образом. Представим, что объект из одного допустимого состояния y переходит в другое допустимое состояние x. Происходит качественный скачёк, индуцируемый некоторой функцией активации внутренних параметров данного состояния, структурными сдвигами. Геометрически этот переход представим как непрерывный процесс поворота системы координат в пространстве X, построенной в виде многогранника Френе. Ограничиваясь ускорениями первого порядка, получаем систему координат как естественный трёхгранник Френе, в котором вектор y определяет одну из координатных осей и в которой вектор x фиксируется двумя полярными углами q и j так, что его можно рассматривать в качестве единичного комплексного вектора x = [a, b]' = [cos q /2; e ij sin q /2]. Если записать квадрат меры |µ|2 = y*M(x)y, то приходим к заключению, что оператор плотности - матрица M(x) = [aa* ab*; ba* bb*], описывает чистое состояние x, т.к. M2 = M . Поскольку орбитальный момент отсутствует, то представим его тождественным оператором поворота I, а поворот вектора y определим спином s = 1/2s, где оператор s = (si| i = 1, 2, 3) выражается через матрицы Паули (|s| = 1/2). Тогда оператор плотности M, определяющий полный момент объекта со следом равным единице, можно записать в виде
M = xs + 1/2I.
Условие M2 = M будет выполняться, если ||x||2 = 1. Координаты вектора x в исходной системе определяются через его компоненты a и b по формулам:
x1 = |a|2 - |b|2 = cos q, x2 = 2Re(ba*) = sin q cos j, x3 = 2Im(ba*) = sin q sin j.
С помощью оператора плотности можно рассматривать системы, которые не приводятся к "чистым состояниям" как, например, динамический вариант объектов финансовой системы – системы банков. Здесь значения наблюдаемой величины A усредняются по её квантовым состояниям - локальным параметрам квантования: капиталу банка, активам, кредитам, депозитам и т.п. Полученные же средние величины ak усредняются по всему ансамблю данных финансовой системы a = pkak. Где pk является вероятностью обнаружения средней величины ak в данном ансамбле и в сумме равны единице. Последнее даёт возможность ввести обобщённый оператор плотности M = pkMk, след которого равен единице и a = Tr(MA), но для которого условие M2 = M уже выполняться не будет.
14. Селективные свойства оператора плотности.
Соотношение M(ej)x = xjej показывает, что если X банахово пространство и последовательность {ej: j Î N} является его базисом, то на данной последовательности можно построить оператор M, для которого элементы ej будут собственными элементарными состояниями, определяющиеся как чистые состояния, для которого справедливы свойства
M(ej)M(ek) = djkM(ek), åj Î N M(ej) = I,
а действие оператора M(ej) на любой элемент x Î X выделяет в нём количество xj элементарного качества, которое определяется волновой функцией Fj = e j.
Обозначим символом X аффинное множество (множество объектов, событий), а символом X - присоединённое к нему векторное пространство (пространство всевозможных допустимых состояний данных объектов). Таким образом, если x событие, то x = j(x) будет его описание в карте j = {ej: j Î N}. События x и y называются совместимыми, если предшествующие измерения одной из них не отражаются на измерениях другой. Отсюда следует, что операторы M(x) и M(y) независимы и, если ввести оператор M(xy) для такого составного измерения, в котором одновременно значение x ставится в соответствие событию x, а значение y - событию y, то получаем
M(xy) = M(x)M(y) = M(y)M(x).
Составное событие x называется полным набором событий xk , k Î K, если каждая пара в наборе совместима и не существует никаких других событий совместимых с каждым событием набора, за исключением, быть может, самого события x. Оператор плотности полного составного события x = {x1, x2, …, x|K|} определяется по формуле [10]
M(x) = Õk Î K M(xk).
Величина x является состоянием полного события. В пространстве X оператор M(x) даёт максимально возможное описание составного события с помощью селективных измерений M(xk), k Î K.
Если для измерения состояния объекта x используется эталон y, то состояние объекта, воспринимаемое как x, зависит от эталона и, следовательно, матрица плотности в определении его меры так же будет зависеть от эталона. В этом случае оператор плотности запишем в виде
M(x, y) = xy*.
В случае скалярной меры транзитивность применения эталона y определим равенством
M(x, a)M(b, y) = dab M(x, y).
Пусть a, b, c, d Î X. Тогда метрический функционал µ(a, b) = a*b и оператор плотности M(c, d) = cd* определяются на множестве X´X. Если X n-мерное векторное пространство, то множество значений метрического функционала принадлежит полю K действительных или комплексных чисел, а операторы плотности будут принадлежать множеству ℳ квадратных матриц порядка n2. Если b является эталоном a, а d служит эталоном c, то в силу равенства
µ(a, b)µ(c, d) = a*M(b, c)d
c должно быть эталоном b. Как частный случай отсюда следует, что если b = lc, то
µ(a, b)µ(c, d) = la*M(c)d.
Аналогичное соотношение получаем для операторов
M(a, b)M(c, d) = µ(b, c)M(a, d).
Следовательно, если d служит эталоном c, а c является эталоном a, то d будет эталоном a.
При обозначении. g = M(b, c)d, h = aµ(b, c) Î X, получаем
µ(a, b)µ(c, d) =µ(a, g),
M(a, b)M(c, d) = M(a, h),
т.е. множество ℳ - левый, а K - правый X-модули, которые в рассматриваемом случае связаны при любых a, b, c, d Î X коммутативным отношением
µ(b, c)M(a, d) = M(a, d)µ(b, c).
и если система {ej: j Î N} является базисом пространства X, то система {Ma = M(ei, ej) : i, j Î N} будет базисом пространства X´X. Любой элемент A Î X´X можно разложить по данному базису. В a-представлении это разложение принимает вид
A = AaMa.
Здесь суммирование осуществляется по всем значениям мультииндекса a = (i, j) Î N´N, а коэффициенты разложения определяются как коэффициенты Фурье
Aa = µa(A) = ei* Aej = = Tr (AMa*) , Ma* = (Ma)* = M(ej, ei), a = (i, j), a* = (j, i).
Для произведения операторов A и B = BbMb, b = (k, l), в a-представлении получаем (g = (i, l))
AB = åjÎNdkjµa(A)µb(B)Mg,
где
µa(A) = eiAej
и для эрмитово сопряжённого базисного элемента введено обозначение
ei = ei*.
Отсюда находим
µg(AB) = åjÎN d kj µa(A)µb(B) = å k Î N mkl(B)mik(A).
Это формула вычисления элемента произведения матрицы B на матрицу A.
Предположим, что наблюдаемая A оценивается в метрике F величиной a = F*AF и I – тождественный оператор, IA = AI = A. Тогда оценку можно записать в виде a = F*IAF, а её единицу факторизовать в виде 1 = F*F = F*IF. При этом тождественный оператор запишется произведением метрических функций
I = FF*.
Дифференцируя оценку тождественного оператора, с учётом уравнений Шредингера, для метрической функции и её сопряжённой, приходим к равенству
0 = F*(¶ t I +1/ih (H + H*)I)F,
из которого заключаем, что тождественный оператор удовлетворяет волновому уравнению
ih ¶ t I = (`H – H)I.
Если известны собственные функции Fk = jkexp(-iEkt/h) гамильтониана, то этот оператор представим функциональным рядом
I = å k,lÎN lkljl*jkexp(-i(El – Ek)t/h) = å,lÎN lkljl*jkexp(-iwlkt), wlk = (El – Ek)/h,
который в оценках играет роль матрицы плотности. Для произвольной наблюдаемой A получаем ряд Дирихле (или ряд экспонент [12])
a = å,l,kÎN lklalkexp(-iwlkt), alk = jl*Ajk , wlk = wl - wk .
16. Оценки в локальных алгебрах.
Точная количественная оценка состояния системы по эталону возможна только тогда, когда она по качеству сопоставима с эталоном, т.е. если x = aΨ, а y =bΨ. Принимая, что функция качества нормирована – Ψ*Ψ = 1, заключаем, что μ = y*x = |ba|. Если b = 1, то μ = |a|. Когда эталон фиксирован, то он неявно присутствует в оценке состояния x = aΨ и его норма определяется выражением ||x|| = (x*x)1/2 = |a|. В противном случае за счёт качественного расхождения появляется ортогональная характеристика – характеристика качественного расхождения ν2 = ||x||2 – a2, дисперсия, которая является мерой вариации, колеблемости наблюдаемой.
Нейронная форма восприятия сознанием явлений окружающей действительности представляется их бинарной оценкой [13], где на каждом k-ом синапсе нейрона (k Î N = 1,2, …) реализуется одна из составляющих k-ой антимонии ak = {ek , ek = ek*}, ak* = {ek*, (ek)*} = {ek, ek} .
Предположим, что на атласе A = {ak: k, l Î N = 1, 2, …} состояние объекта и эталон имеют, соответственно, представления y = G(y)e, x = A(x)y = A(x)G(y)e. Получаем оценку объекта
μ = μ(x, y) = e*M(x,y)e, M(x, y) = G*(y)A(x)G(y),
т.е. оценка есть средняя величина оператора M = M(x, y). Унитарный оператор G = G(y) является фундаментальным метрическим тензором в окрестности действия данного эталона и от состояния объекта не зависит. Этот оператор определяет локальную систему координат в окрестности фиксированного эталона. Наблюдаемая связана с плотностью оценки обратным преобразованием
A(x) = G(y)M(x, y)G*(x).
Отсюда находим дисперсионную оценку отклонения состояния от эталона
ν2(x, y) = y*(D(y)A* - AD(y))x.
Все входящие в эти равенства величины могут рассматриваться как тензоры, а операции над ними – как тензорные операции. Естественно, что структура этих величин определяется формой задания эталона, который, в общем случае, в n-мерном метрическом пространстве может быть тензором n-го ранга [14].
17. Оценки в полярном представлении
В стандартной полярной системе координат произвольный элемент имеет представление x =s exp(iq/h). Аналогичное представление имеет и фиксирующий единицу измерения эталон yo = soexp(iqo/h). В локальных координатах окрестности эталона этот элемент будет иметь представление x = y*x/|y| = s exp(ij/h), где j = q - qo, т.е. в окрестности эталона фиксируется фаза отсчёта, а оценка m = y*x получается его умножением на амплитуду эталона.
Сравним в полярном представлении в окрестности эталона два произвольных элемента x = a exp(ia/h) и y =b exp(ib/h). Для окрестности эталона (соответствующей карты) введём обозначение Uo и в данной карте введём локальную алгебру, рассматривая её элементы как множество комплексных чисел. Тогда в данной карте каждому элементу x будет отвечать комплексно сопряжённый элемент x* = a exp(-ia/h) и можно полагать действительными все операции над элементами карты Uo в пространстве комплексных чисел C.
Каждый элемент карты представим в экспоненциальном виде
x = exp(ix/h), y = exp(ih/h), x = a - ih ln a, h = b - ih ln b.
Тогда произведения элементов имеют представления
xy = exp(i(x + h)/h), xy* = exp(i(x +h*)/h), h* = - h,
а их произведение степеней, например, функции
f = CÄ xaÄ yb = exp(ij/h),
имеют представление
f = exp(i(ax Å bh Å ih ln C)/h,
Это позволяет сводить задачи экономического анализа с нелинейными функциональными зависимостями [5] к задачам анализа в линейных пространствах [15]. Естественно, нелинейную функцию здесь аппроксимировать рядом Дирихле, формальным степенным [16] или позиномиальным рядом [17]
f = å kÎM ak fk(x) = å kÎM ak PlÎN xla(k, l), ak, a(k, l) = akl = Î C.
18. Производственные функции типа Кобба-Дугласа.
В первой половине девятнадцатого века Огюст Конт в своём "Курсе позитивной философии" писал, что "изучая развитие человеческого разума... от первого его проявления до наших дней, думаю, я открыл великий основной закон, по которому с неизменной необходимостью можно установить как путем наших рациональных доказательств, так и путем внимательного анализа прошлого, историческую достоверность. Этот закон состоит в том, что каждое из наших основных понятий проходит, необходимым образом, три теоретически различных стадии: стадию теологическую, или фиктивную; стадию метафизическую, или абстрактную; стадию научную, или позитивную... Отсюда три типа философии, или концептуальных систем, обобщающих феномены, взаимно исключающих друг друга. Первая — начальный пункт, необходимый для человеческого понимания (intelligentia), третья — фиксированная и определенная стадия, а вторая уготована служить в качестве транзитного пункта". Этот закон представим диаграммой
П ® Т ® И.
Таким образом, абстрактная, позитивная (рассудочная) логика является сердцевиной любой науки, любой философии. Эта часть в отражении является анализом и опирается на количественные сравнения взаимоотношений закономерностей развития мира. Здесь применяются абстрактные, математические методы анализа. Уместно процитировать слова великого философа, физика и математика восемнадцатого века Эммануила Канта, что "в каждой науке столько науки, сколько в ней математики". Лишившись этого "транзитного пункта", любая философия лишается своего образа как науки. Действительно, оценить товар при экономической сделке или криминальность поступка человека можно только путём сравнения с другими товарами или с поведением окружающих данного человека других людей. При этом такое сравнение строится на многообразии наблюдений, их статистической обработкой.
Следовательно, научный анализ любого вида деятельности предполагает построение математической зависимости результатов от обусловивших их факторов. Но, как правило, из-за бесконечности структуры K результаты, показатели высшего уровня деятельности, могут оказаться
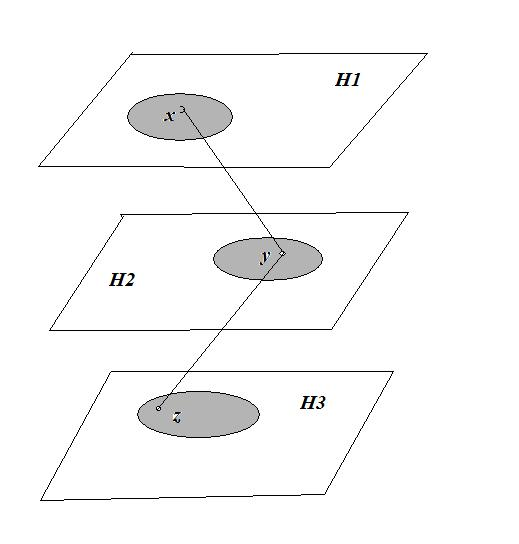
Рис.1. Структура категории.
оказаться очень далекими от граничных факторов, если не говорить об их бесконечной удалённости. Поэтому, влияние отдельного фактора на конечные результаты высшего уровня иерархии многоэшелонированной структуры может оказаться за горизонтом видимости.
Выделим три слоя структуры K (рис. 1) H1,H2, H3. На первом слое H1 возьмём произвольный объект x Î K. На слое H2 выделим объекты K , находящиеся на орбите объекта x и выделим из них произвольный элемент y Î K (x). Определим их бинарным отношением a, т.е. (y, x) = yax Î a , или
Ka(x) = {y Î K | yax}.
Аналогично построим множество
Kb(x) = {z Î K | zby}.
Будем полагать, что объекты Kb(x), находящиеся на орбите элемента x на слое H3, лежат за горизонтом видимости.
Пусть на структуре категории K определён функтор P(K ). Тогда существуют функциональные зависимости
P(x) = fa(P(y)| y Î Ka(x)), P(y) = fb(P(z)| z Î Kb(y)),
обеспечивающие факторную свёртку в соответствующий показатель. Из-за свёртки действие отдельных объектов структуры слоя H3 на результирующий показатель P(x) неразличимы. Однако существует композиция
P(x) = (fa◦fb)(P(z)| z Î Kb ◦a(x)),
позволяющая различить влияний фактора любого среза на результирующий показатель. Но, расстояние от граничного среза до результирующего слоя может быть настолько большим, что вариация этого фактора на изменение показателя практически не оказывает существенного влияния. Локальная же корреляция может быть не только существенной, но и нелинейной.
Любая функция в стратифицированной схеме может быть как линейной, так и нелинейной. Если функция fa линейная, а функции fb нелинейные, то нелинейную многофакторную линеризацию можно провести в логарифмических шкалах, тогда результирующую иерархическую зависимость можно представить позиномом. Каждый член позинома является степенной функцией – функцией типа Кобба-Дугласа, которая в большинстве первых работ использовалась для анализа физических отношений между результатами и факторами производственной деятельности [18].
Применение в многоэшелонированном моделировании позиномиальных моделей удобно для проведения факторного анализа. Пусть, например,
f = å kÎM akfk(x1, x2, …, xn),
где fk – функция типа Кобба-Дугласа. Учитывая, что xl¶ fk /¶ xl = fk , и вводя обозначения akfk / f = lk , для эластичности агрегатного показателя по l –му фактору xl получаем выпуклую линейную комбинацию
e l (f) = å kÎM lka kl , l k > 0, å kÎM lk = 1.
19. Оператор конечного смещения.
При постановки задач стратегического планирования и управления часто приходим к задачам преследования подвижных целей. Допустим, что x – цель стратегического планирования, y – тактический план сближения с целью, а u = vt – управляющий вектор, т.е. x = y + u. Эволюция каждой переменной описывается своим уравнением
ih ¶ x / ¶ t = H(x)x, ih ¶ y / ¶ t = H(y)y,
которые полностью определяются гамильтонианами. Задача преследования заключается в достижении предела в соотношении H(y) → H(x) = H(y + u).
Стратегическую цель разложим по степеням разностей x – u = u и свяжем градиент с импульсом тактического действия равенством Ñy = ip / h. Будем иметь:
x = å¥n=0 1/n! (u*Ñy)ny = å¥n=0 1/n! (i u*p / h)ny = exp(i u*p /h) y = Ty.
Унитарный оператор, оператор смещения T = А(u, p) = exp(i u*p /h), действует в карте эталона. Определим его как T = T(y). Если умножить уравнение Шредингера для эталона слева на этот оператор и ввести обозначение (¶ y / ¶ t)T = -iTH(y)y / h, то придём к уравнению
ih (¶ y / ¶ t)T = HT(y)x, HT(y) = T(y)H(y)T-1(y).
Поскольку y = T-1x, то отсюда находим
H(x) = HT(y) + ih (¶ T /¶ t)T-1,
или
H(x) = A(u, p)H(y)A*(u, p) – v*p.
Таким образом, сближение будет зависеть от модулей векторов скорости сближения и импульса и от их направления друг относительно друга.
20. Понятия о напряжённом и деформированном состоянии системы.
Рассмотрим некоторую структуру K . На этой структуре определим метрический тензор Y = Y(K) и два состояния y = y(K) = BY и x = x(K). Состояние y определим как расчётное, оптимальным образом учитывающее внутренние особенности структуры, т.е. учитывающее наискорейшее изменение состояния при её нагрузке. В таком случае будем предполагать, что тензор B пропорционален градиенту Ñ = Ñ(K), B = bÑ. Состояние x = x(K) определим как фактическое состояние системы, которое она приняла при приложении расчётной нагрузки из-за её внутренних особенностей, внутреннего трения (взаимоотношения между её элементами). Будем предполагать, что данные состояния достаточно близки, т.е. имеет место представление x = y + u, где возмущение u = u(K) мало. Основа этих допущений приведена на рис.2
Здесь исходное состояние системы отображается точкой M0 эквипотенциальной поверхности P0 (Ψ = const); H0 - касательная плоскость этой точке к поверхности. По расчётным данным предполагается, что при дополнительном приложении усилий,
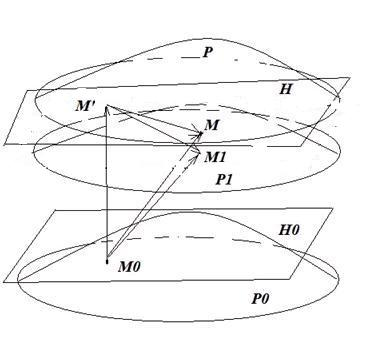
Рис.2. Геометрическая интерпретация приближённого равенства при сравнении напряженного состояния системы.
эквивалентных вектору y = M0M' система перейдёт на более высокий энергетический уровень P в состояние, отвечающее точке M' (y = b grad Ψ), лежащей на поверхности P. Но фактически, из-за потери приложенных усилий на внутренних связях, система переходит в состояние x', на поверхность P1 с более низким энергетическим потенциалом, отображаемое на представленном рисунке вектором M0M1. Если провести касательную плоскость H к поверхности P в точке M' и точку M1 спроектировать на эту плоскость (полагая, что точка M является основанием данного перпендикуляра), то можно заметить, что треугольники DM0M'M и DM0M'M1 мало отличаются друг от друга. Отметим, что их сходство будет тем больше, чем меньше кривизна поверхности P. Полагая M'M1 = u', а M'M = u, подменяем соотношение x' = y + u' равенством x = y + u.
Состояние системы обусловлено внутренними факторами взаимодействия объектов системы, т.е. состоянием объектов и состоянием связей между данными объектами структуры K (объектов и морфизмов категории K). При нагружении системы она переходит в возбужденное состояние. В её узлах и на связях между ними возникают "силовые" нагрузки, которые характеризуют состояние любого сечения системы и взаимоотношения между нижними и верхними её эшелонами по отношению фиксированного слоя. При различных нагрузках системы меняются и силовые факторы на каждом сегменте структуры, т.е. на её узлах и связях. Происходит переход системы из одного состояния в другое, который свидетельствует об изменении качества системы.
Возможны два варианта изменения качества. В первом варианте силовые нагрузки в узлах и связях не превышают предельные. Качественное изменение системы не приводит к изменению её структуры. В этом случае будем полагать, что такие состояния являются допустимыми. Для таких состояний на структуре K можно построить определённую метрическую систему Y. Во втором случае нагрузка в отдельных элементах системы становится не только особо опасной, но и может быть запредельной, приводящей к разрушению этих элементов. Если система не разрушается, то это приводит к структурной перестройке. Появляется новая структурная схема K ' нового метрического качества Y ' при частично несравнимом круге единиц [4, стр.35] относительно старого качества.
Функтор x = x(K) определяет напряжённое состояние системы. И если зафиксировать два произвольных иерархических среза структуры Ka и Kb , где a < b, на срезе Ka взять произвольную точку k, а на срезе Kb выбрать полную группу её орбитальных объектов Kb (k), то, полагая, что состояние объекта xk(a) системы определяется обратным спектром, т.е. состоянием её орбитальных объектов на b-срезе, заключаем, что напряжённое состояние k-го объекта среза Ka (как терминального объекта категории K ) представимо с b-горизонта вектором полного напряжения
xk(a) = (xk1(b); xk2(b); …; xkn(b)), k Î Ka, b Î Kb(a), a, b Î A,
где для иерархической классификации слоёв структуры введено обозначение A .
Предположим, что расчётный функтор y = y(K)Î Y определяет нормальное состояние системы, а функтор x = x(K) Î X – её фактическое состояние. Тогда на бинарном соответствии z = (X, Y, Z Í X´Y) можно определить метрическую функцию m(z) = m(x, y) = y*x, характеризующую сходство напряжённых состояний данной системы, и функцию n(z) = n(x, y), характеризующую расхождение этих состояний. Индикатор
Iy(x) = m(x, y)/D(y), D(y) = m(y, y),
определяет коэффициент напряжённости фактического состояния системы по отношению к её расчётному состоянию. В свою очередь, его можно рассматривать как функтор, определённый на категории K , который на каждом объекте структурной схемы системы характеризует коэффициент напряжённости как среднюю величину коэффициентов напряжённости объектов его орбиты на видимом горизонте, т.е.
Iy(xk) = å {llk Iy(xkl): l Î Ky(xkl)}, llk = m(xkl, ykl)/D(yk) ³ 0, å {llk : l Î Ky(xkl)} = 1.
Изменение нагрузки в узлах по отношению к её расчётным значениям ведёт к изменению весовых коэффициентов объектов орбиты в агрегатной формуле, т.е. приводит к изменениям количественных оценок связей системы, что воспринимается как деформирование её структуры без изменения её метрических основ.
Зная коэффициенты напряжённости на каждом объекте, можно найти критические элементы системы – те опасные точки системы, которые ведут к микроразрушениям в её структуре, т.е. система после снятия запредельной нагрузки не восстанавливается. Меняется её структурное качество, конечным результатом таких нагрузок может быть разрушение системы, ликвидация её предназначения.
Выделим произвольный объект структуры K. Пусть это k-объект a-слоя и yk(a) его нормальное расчётное напряжённое состояние при заданной нагрузке системы. Фактически же напряжённое состояние этого объекта при той же нагрузке системы стало xk(a). Имея представление об эволюции напряжённого состояния (рис. 2), дадим более простую интерпретацию, которую представим рис. 3.
Здесь предполагается, что выделенный объект в исходном напряжённом состоянии находился в точке M0 и имел производственный потенциал на уровне H0. По расчётным данным после изменения нагрузки на систему фиксированный объект должен был перейти на энергетический уровень H1, приобретя напряжённое состояние y. Однако, в силу внутренних связей, он перешёл на уровень H, обретя напряжённое состояние x. Если уровни H1 и H достаточно близки, то треугольники M0M'M и M0MM'' мало отличаются друг от друга, а, следовательно, можно полагать, что M0M'' ~ M'M = u и M''M ~ M0M' = y, т.е. полагать, что приближённо выполняется равенство x = y + u. Отсюда заключаем, что вектор фактического напряжения в данном объекте системы раскладывается на две составляющие: нормальное напряжение y и составляющую u, которую назовём касательным напряжением.
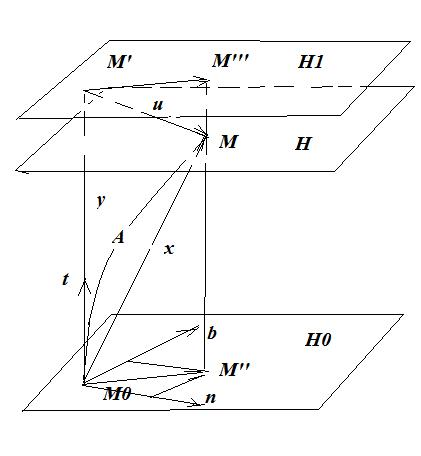
Рис.3. Интерпретация динамики напряжённого состояния системы
в трёхмерном пространстве.
Если известна кривая изменения напряжённости на данном объекте системы, кривая M0AM, то вектор напряжения x можно разложить по составляющим натурального подвижного трёхгранника
xk(a) = yk(a)tk(a) + unk(a)nk(a) + ubk(a)bk(a),
где n – вектор нормали к траектории эволюции напряжённого состояния, b= t´n –бивектор.
Для дальнейшего анализа запишем данное равенство в виде
xk(a) = xsk(a)eks(a),
где введём обозначения для коэффициентов
x1k(a) = yk(a), x2k(a) = unk(a), x3k(a) = ubk(a)
и направляющих векторов
ek1(a) = tk(a), ek2(a) = nk(a), ek3(a) = bk(a).
Его, как вектор напряжённости k-го терминального объекта a-среза структуры, можно также представить в виде разложения по качественным признакам напряжённости орбитальных объектов b-среза
xk(a) = xlk(b)ekl(b),
где суммирование проводится по всем l Î Nk(b) и N(b) = å k Î N(a) Nk(b).
Пусть X(K) – определённое на структуре K некоторой системы множество её допустимых напряжённых состояний; x(K) и n(K) – два произвольных состояния из (X, m) – метрического пространства X с мерой m. Произвольно выделим на структуре K два слоя a и b. На слое a возьмём произвольный объект k Î N(a), а на слое b выделим полное множество его орбитальных объектов Nk(a). Напряжённые состояние объекта k Î K, видимое с горизонта b, для упрощения анализа запишем в виде
x = xlel, n = nlel.
Положим, что n нормальное состояние выделенного объекта и m(n, n) = 1, а напряжённое состояние x получено возмущением его нормального состояния. Принимая, что возмущённое состояние достаточно мало отличается от исходного, заключаем, что существует линейный оператор s: X → X такой, что
x = sn.
Проектируя, теперь, состояние x на направление n, получаем градуированную шкалу для оценки произвольных напряжённых состояний из окрестности данного нормального состояния. Оператор возмущения s называется тензором напряжения и построенная шкала, по существу, будет оценочной шкалой тензора напряжений выделенной данным фиксированным элементом как терминальным объектом структуры с соответствующим ограниченным видимым горизонтом подструктуры.
Любое напряжённое состояние по качеству действия можно разложить на две составляющие. Одна из составляющих y характеризует объект по отношению содержания в нём качественных признаков нормального состояния, другая u – ортогональная касательная составляющая, характеризует новые приобретённые качественные признаки, т.е.
x = y + u.
Эти составляющие можно выразить через известные характеристики тензора напряженного состояния и составляющие нормального напряжения системы.
Действительно, поскольку u*y = 0, то компонентами y будут служить соответствующие средние величины тензора напряжений
y = (n*sn)n,
а поскольку из равенства u = x – y следует
u = (s - n*sn)n,
то в ковариантном базисе они имеют представления
ys = sjk nj nk ns, us = (s ks - s sl nl nk )ns.
Как всякий тензор второй валентности, тензор напряжения s можно разложить на шаровой тензор 𝓢(s) и девиатор 𝓓(s). Шаровой тензор до скалярного множителя совпадает с метрическим g тензором. Если метрический тензор определить равенством n*gn = n*n и положить степень свободы выбранного терминального объекта равной n, то получим представление
s = 𝓢 + 𝓓,
где
𝓢 = so g, so = 1/n Tr s.
Из соотношений
s n = ln, 𝓓 n = (l - so )n
заключаем, что главные направления тензора напряжений и его дивиатора совпадают, а их главные значения отличаются на постоянную величину so равную средней величине собственных значений тензора напряжений; при этом вектор касательного напряжения зависит только от девиатора тензора напряжений и имеет вид
u = (𝓓(s) – n*𝓓(s)n)n.
Рассмотрим некоторую систему. Пусть её состояние описывается величиной xo. Как любая величина она определяется количеством определённого качества. Величину, характеризующую состояние системы, запишем в виде
xo = xoe.
Качественная характеристика e определяет систему координат (карту) в окрестности точки, заданной фиксацией состояния системы, т.е. задает направление и масштаб отсчёта каждого элементарного качественного признака {e1,e2, …}, входящего во множество e, при изменении состояния системы.
Предположим, что система из данного фиксированного состояния по расчётным данным должна перейти в состояние y, но, в силу некоторых неучтённых внутренних особенностей, фактическим состоянием её становится состояние x. Будем полагать, что как расчётное состояние, так и фактическое её состояния можно рассматривать в той же карте, т.е. отклонение фактического состояния от расчётного мало, мала величина u в выражении
x = y + u.
Очевидно, дополнительное слагаемое правой части имеет то же качество, что и его составляющие, т.е. если x = xe и y = ye, то
u = x – y = ue,
а величины, x, y и u, которыми описываются количественные характеристики состояний, являются соответствующими тензорами одинаковой валентности.
Фактическое состояние от расчётного отличается тем, что в фактическом состоянии произошли внутренние качественные изменения, отличные от расчётных. Эти отклонения будем называть деформацией системы. Определим равенством
D(x) = (1 +2e(x, y))D(y)
коэффициент деформации
e = (D(x) – D(y))/2D(y).
Коэффициент деформации связан с гамильтонианом равенством
H(x, y) = ½ D(x)/D(y) = ½ +e,
т.е. коэффициент деформации разложим в произведение сопряжённых функций
e = F*F, F = (m +in)/21/2, F = (m - in)/21/2
и является простейшим гармоническим осциллятором [7, стр. 61].
Определим характеристику деформаций системы через исходные величины тензоров состояний. Будем иметь
e D(y)=( D(x) – D(y))/2 = {e*[(y +u)*(y +u) – y*y]e}/2 = e*𝓔e,
где тензорная величина
𝓔 = (y*u + u*y + u*u)/2
определяется как тензор деформации системы. Из его конструкции видим, что тензор деформации является самосопряжённым оператором 𝓔* = 𝓔 и при малых деформациях можно ограничиться равенством
𝓔 = (y*u + u*y)/2.
В силу самосопряжённости все собственные функции тензора деформации ортогональны, а все его собственные значения вещественны.
Таким образом, усилия, приложенные к граничным элементам системы и отличные от нормальных, вызывают деформацию её структуры. Деформация системы распределяется по структурным связям между её элементами, изменяет силу этих связей.
Если рассматривать состояние системы как функцию точки M (рис. 3) в некотором потенциальном поле, то расчётное состояние, отвечающее вектору y прикреплённому к точке M0, будет определяться наибольшей скоростью роста потенциала системы, градиентом функции состояния. Этот факт отметим соотношением y = bÑ. В этом случае тензор деформации можно представить в виде
𝓔 = b(Ñ*u + u*Ñ)/2
Если ввести по формуле
Ñ = ip/h
связь градиента с импульсом, то выражение для тензора деформации принимает вид
𝓔 = ib(p*u + u*p)/2h.
С другой стороны, из равенства
e*𝓔e = D(y)F*F
следует, что существует линейный оператор W такой, что y = s(y)F = We, для которого имеет место разложение
𝓔 = W*W
и из которого следует, что оператор W является оператором преобразования координат.
Пусть система, обладающая исходным свойством Ψ, подвергается деформации 𝓔 и переходит в состояние x, т.е. x = 𝓔Ψ. Деформацию системы можно представить прямой суммой трансляции y и вращательной симметрии u, т.е.
x = y + u.
Поскольку при трансляции свойства системы не меняются, то находим
y = yΨ,
где количественная характеристика определяется выражением
y = m(x, Ψ) = Ψ*𝓔Ψ
Тогда для составляющей вращательной симметрии имеем
u = x – y = 𝓔Ψ – (Ψ*𝓔Ψ)Ψ.
25. Сдвиг наблюдателя.
1. Идлис Г.М. Единство естествознания по Бору и единообразные взаимосвязанные периодические системы физики, химии, биологии и психологии /Исследования по истории физики и механики, 1990 //М., Наука, 1990.
2. Федорчук В.В., Филиппов В.В. Общая топология /Изд. МГУ. 1988.
3. Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем /М., Мир, 1973.
4. Адамов В.Е. Факторный индексный анализ /М., Статистика, 1977.
5. Маслов В.П. Нелинейное среднее в экономике /Мат. заметки, 2005, т.78, вып. 3.
6. Ландау Л.Д.Б Лифшиц Е.М. Квантовая физика, т. Ⅲ /М., Наука, 1989.
7. Грин Х. Матричная квантовая алгебра /М., 2010.
8. Хайкин С. Нейронные сети /М., С.-Петербург, Киев, 2008.
9. Кемпфер Ф. Основные положения квантовой механики /М., 2007.
10. Швингер Д.С. Квантовая кинематика и механика /М., Наука, 1992.
11. Берже М. Геометрия /М., Мир, 1984.
12. Леонтьев А.Ф. Ряды экспонент /М., Наука, 1976.
13. Хайкин С. Нейронные сети /М., С.-П., Киев, 2008.
14. Димитриенко Ю.И. Тензорное исчисление /М., 2001.
15. Арсеньев Ю.Д. Теория подобия в инженерных экономических расчётах /М., 1967.
16. Грауэрт Г., Реммерт Р. Аналитические локальные алгебры /М., 1988.
17. Даффин Р., Питерсон Э., Зенер К. Геометрическое программирование /М., 1972.
18. Терехов Л.Л. Производственные функции /М., 1974.
19.